题目内容
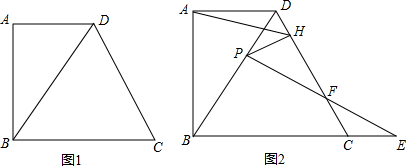
19.如图,已知在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=3,sin∠BCD=$\frac{2\sqrt{5}}{5}$,点P是对角线BD上一动点,过点P作PH⊥CD,重足为H.(1)求证:∠BCD=∠BDC;
(2)如图1,若以P为圆心,PB为半径的圆和以H为圆心、HD为半径的圆外切时,DP的长;
(3)如图2,点E在BC延长线上,且满足DP=CE,PE交DC于点F,若△ADH和△ECF相似,求DP的长.
分析 (1)作DQ⊥BC,在直角△CDQ中利用三角函数即可求解;
(2)设DP=x,当⊙P与⊙H外切时,PH=DH+BP,据此即可列方程求得;
(3)作PM∥BE,分△ADH∽△FCE和△ADH∽△ECF两种情况进行讨论,依据相似三角形的对应边的比相等求解.
解答 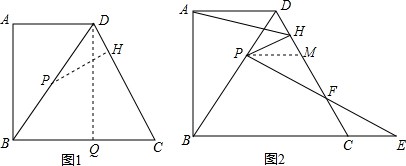 解:(1)作DQ⊥BC,
解:(1)作DQ⊥BC,
∵BQ=AD=3,DQ=AB=4,
∴CD=$\frac{DQ}{sin∠BCD}$=2$\sqrt{5}$,CQ=2,
∴BC=5=BD,
∴∠BCD=∠BDC;
(2)设DP=x,则DH=$\frac{\sqrt{5}}{5}$x,PH=$\frac{2\sqrt{5}}{5}$x,BP=5-x.
当⊙P与⊙H外切时,PH=DH+BP,
即$\frac{2\sqrt{5}}{5}$x=$\frac{\sqrt{5}}{5}$x+5-x,
解得:x=$\frac{25-5\sqrt{5}}{4}$;
(3)作PM∥BE.
则PM=DP=x,DH=HM=$\frac{\sqrt{5}}{5}$x,
由$\frac{PM}{CE}$=$\frac{FM}{CF}$=1,CF=FM=$\sqrt{5}$-$\frac{\sqrt{5}}{5}$x,
当△ADH∽△FCE时,$\frac{AD}{CF}=\frac{DH}{CE}$,
即$\frac{3}{\sqrt{5}-\frac{\sqrt{5}}{5}x}$=$\frac{\frac{\sqrt{5}}{5}x}{x}$,
解得:x=-10(舍去).
当△ADH∽△ECF时,$\frac{AD}{CE}$=$\frac{DH}{CF}$,
即$\frac{3}{x}$=$\frac{\frac{\sqrt{5}}{5}x}{\sqrt{5}-\frac{\sqrt{5}}{5}x}$,
解得:x=$\frac{-3+\sqrt{69}}{2}$.
∴DP的长是$\frac{-3+\sqrt{69}}{2}$.
点评 本题考查了三角函数以及相似三角形的判定与性质和圆外切的性质,正确分成△ADH∽△FCE和△ADH∽△ECF两种情况进行讨论,求得x的值是关键.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | AD=BC | B. | AC=BD | C. | ∠A=∠C | D. | ∠A=∠B |
 二次函数的图象如图所示,则其解析式为y=-x2+2x+3.
二次函数的图象如图所示,则其解析式为y=-x2+2x+3.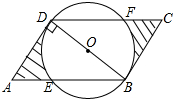 如图,平行四边形ABCD中,AB=6,AD=3,BD⊥AD,以BD为直径的圆交AB于E,交DC于F,则阴影部分的面积$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.
如图,平行四边形ABCD中,AB=6,AD=3,BD⊥AD,以BD为直径的圆交AB于E,交DC于F,则阴影部分的面积$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.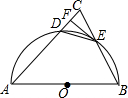 如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.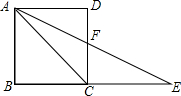 如图,正方形ABCD,AC=CE,则∠DAF=22.5°.
如图,正方形ABCD,AC=CE,则∠DAF=22.5°.