题目内容
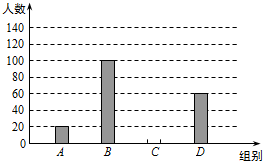
9. 二次函数的图象如图所示,则其解析式为y=-x2+2x+3.
二次函数的图象如图所示,则其解析式为y=-x2+2x+3.
分析 根据图象可知,抛物线对称轴是直线x=1,与y轴交于(0,3),与x轴交于(-1,0),设出一般式,列出方程组求出系数即可.
解答 解:由图象可知,抛物线对称轴是直线x=1,与y轴交于(0,3),与x轴交于(-1,0)
设解析式为y=ax2+bx+c,
$\left\{\begin{array}{l}{-\frac{b}{2a}=1}\\{c=3}\\{a-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$.
故答案为:y=-x2+2x+3.
点评 本题考查的是待定系数法求二次函数的解析式,根据题意找出特殊点、列出方程组是解题的关键,解答时,要认真审题,找准特殊点,才能得到正确的方程组.

练习册系列答案
相关题目
17.下列事件是确定事件的是( )
| A. | 阴天一定会下雨 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 在五个抽屉中任意放入6本书,则至少有一个抽屉里有两本书 |
14.下列各数中,整数部分为3的数是( )
| A. | π | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
1.如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,点A,B在直线l上.将Rt△ABC沿直线l向右作无滑动翻滚,则Rt△ABC翻滚一周时点A经过的路线长是( )


| A. | 5π | B. | $\frac{3π}{2}$ | C. | $\frac{13π}{2}$ | D. | $\frac{23π}{2}$ |