题目内容
10.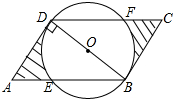 如图,平行四边形ABCD中,AB=6,AD=3,BD⊥AD,以BD为直径的圆交AB于E,交DC于F,则阴影部分的面积$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.
如图,平行四边形ABCD中,AB=6,AD=3,BD⊥AD,以BD为直径的圆交AB于E,交DC于F,则阴影部分的面积$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.
分析 根据题意得出阴影部分面积为:2(S△ADB-S扇形DOE-S△BOE)进而求出即可.
解答 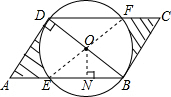 解:连接EO,FO,过点O作ON⊥BE于点N,
解:连接EO,FO,过点O作ON⊥BE于点N,
∵AB=6,AD=3,BD⊥AD,
∴∠ABD=30°,
则∠DOE=60°,
故BD=ABcos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
则BO=$\frac{3\sqrt{3}}{2}$,ON=$\frac{3\sqrt{3}}{4}$,BN=$\frac{9}{4}$即BE=$\frac{9}{2}$,
故阴影部分面积为:2(S△ADB-S扇形DOE-S△BOE)=2[$\frac{1}{2}$×3×3$\sqrt{3}$-$\frac{60π×(\frac{3\sqrt{3}}{2})^{2}}{360}$-$\frac{1}{2}$×$\frac{3\sqrt{3}}{4}$×$\frac{9}{2}$]=$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.
故答案为:$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.
点评 本题主要考查了扇形面积求法,理解阴影面积等于三角形面积减扇形面积和三角形面积是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
1.如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,点A,B在直线l上.将Rt△ABC沿直线l向右作无滑动翻滚,则Rt△ABC翻滚一周时点A经过的路线长是( )


| A. | 5π | B. | $\frac{3π}{2}$ | C. | $\frac{13π}{2}$ | D. | $\frac{23π}{2}$ |
5.据中新社北京2015年1月8日电,2014年中国粮食总产量达到586 400 000吨,用科学记数法表示为( )
| A. | 5.864×107吨 | B. | 5.864×108吨 | C. | 5.864×109吨 | D. | 5.864×1010吨 |
15.已知⊙O的面积为4π,则其内接正三角形的面积为( )
| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\frac{3}{2}$$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
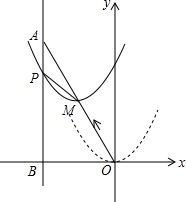 如图,在平面直角坐标系中,已知点A坐标为(-2,4),直线x=-2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(-2,4),直线x=-2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到A点时停止移动.