题目内容
8.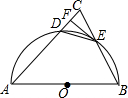 如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.(1)求证:DE=CE;
(2)判断EF与⊙O的位置关系,并说明理由;
(3)若⊙O的直径为18,BC=12,求EF的长.
分析 (1)根据等腰三角形的性质,由AB=AC得到∠B=∠C,再根据圆内接四边形的性质得∠CDE=∠B,则∠CDE=∠C,于是根据等腰三角形的判定即可得到DE=CE;
(2)如图,连接AE、OE,根据圆周角定理,由AB为直径得到∠AEB=90°,再根据等腰三角形的性质得BE=CE,于是可得到OE是△ABC的中位线,所以OE∥AC,由于EF⊥AC,则EF⊥OE,则根据切线的判定定理可判断EF与⊙O相切;
(3)证明Rt△ABE∽Rt△ECF,利用相似比计算出CF=2,然后利用勾股定理计算EF的长.
解答 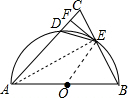 (1)证明:∵AB=AC,
(1)证明:∵AB=AC,
∴∠B=∠C,
∵四边形ABED内接于⊙O,
∴∠CDE=∠B,
∴∠CDE=∠C,
∴DE=CE;
(2)解:EF与⊙O相切.理由如下:
如图,连接AE、OE,
∵AB为直径,
∴∠AEB=90°,
∵AB=AC,
∴BE=CE,即点E是BC的中点,
∴OE是△ABC的中位线,
∴OE∥AC,
∵EF⊥AC,
∴EF⊥OE,
∴EF与⊙O相切;
(3)解:∵AB=AC=18,BC=12,
∴∠B=∠C,BE=CE=6,
∴Rt△ABE∽Rt△ECF.
∴$\frac{AB}{CE}=\frac{BE}{CF}$,即$\frac{18}{6}=\frac{6}{CF}$,解得CF=2,
在Rt△CEF中,EF=$\sqrt{C{E^2}-E{F^2}}=4\sqrt{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的性质、勾股定理和相似三角形的判定与性质.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
13.某市统计局发布的统计公报显示,2006年到2010年,某市GDP增长率分别为9.9%、10.1%、10.3%、10.5%、10.2%.经济评论员说,这5年该的GDP增长率相当平稳,从统计学的角度看,“增长率相当平稳”说明这组数据( )比较小.
| A. | 中位数 | B. | 方差 | C. | 众数 | D. | 平均数 |
14.某运动器械厂根据市场需求,计算生产A、B两种型号的按摩椅,某部分信息如下:A、B两种型号的按摩椅共生产40台,该厂所筹生产按摩椅的资金不少于90万元,但不超过91万元,且所筹资金全部用于这两种按摩椅,现已知A、B两种按摩椅的生产成本和售价如表:
根据以上信息,解答下列问题:
(1)该公司对此两种按摩椅有几种生产方案?那种生产方案获得最大利润?
(2)据市场调查,每台A型按摩椅的售价将会提高a万元(a>0),每台B型按摩椅售价不会改变,该公司应如何生产才可以获得最大利润?
| 型号 | 成本(万元/台) | 售价(万元/台) |
| A | 2 | 2.4 |
| B | 2.5 | 3 |
(1)该公司对此两种按摩椅有几种生产方案?那种生产方案获得最大利润?
(2)据市场调查,每台A型按摩椅的售价将会提高a万元(a>0),每台B型按摩椅售价不会改变,该公司应如何生产才可以获得最大利润?
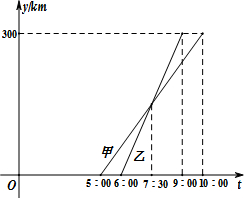 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.
甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.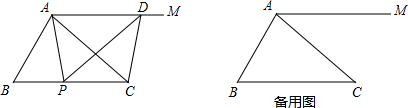
 如图,在平面直角坐标系中,已知点A坐标为(-2,4),直线x=-2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到A点时停止移动.
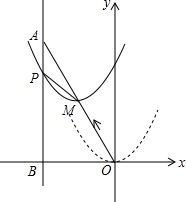
如图,在平面直角坐标系中,已知点A坐标为(-2,4),直线x=-2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到A点时停止移动.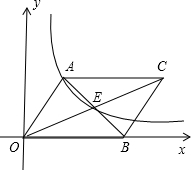 如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.
如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.