题目内容
15.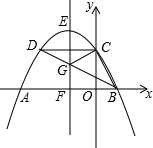 如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.
如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.
分析 连接AG,由二次函数的性质得出A、G、C三点共线,且AF=BF,设抛物线的对称轴为x=m,得出OA=-2m+2,AB=-2m+4,证明△AOC∽△COB,得出OC2=OA•OB,得出方程,解方程得出A的坐标,求出二次函数的解析式,化成顶点式,即可得出结果.
解答 解:连接AG,如图所示: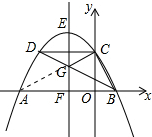
由二次函数的性质得:A、G、C三点共线,且AF=BF,
设抛物线的对称轴为x=m,
∵B(2,0),
∴OF=-m,AF=BF=-m+2,
∴OA=-2m+2,AB=-2m+4,
∵抛物线y=ax2+bx+4交y轴于点C,
∴C(0,4),
∴OC=4,
若△BCG为直角三角形,则∠BCG=90°,
∵OC⊥AB,
∴△AOC∽△COB,
∴OA:OC=OC:OB,
∴OC2=OA•OB,即42=2(-2m+2),
解得:m=-3,
∴OA=8,
∴A(-8,0),
把A(-8,0),B(2,0)代入抛物线y=ax2+bx+4得:$\left\{\begin{array}{l}{4a+2b+4=0}\\{64a-8b+4=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$,
∴抛物线y=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4=-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$;
∴EF的长为$\frac{25}{4}$;
故答案为:$\frac{25}{4}$.
点评 本题考查了抛物线与x轴的交点、二次函数的性质、相似三角形的判定与性质、待定系数法求二次函数的解析式;熟练掌握二次函数的性质,证明三角形相似求出A的坐标是解决问题的关键.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案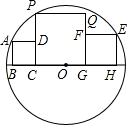 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
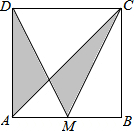 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
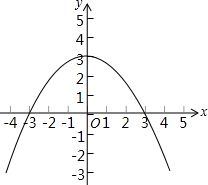 如图,在平面直角坐标系中画出了函数y=ax2+c的图象.
如图,在平面直角坐标系中画出了函数y=ax2+c的图象.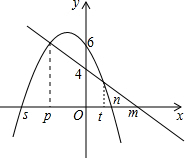 如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).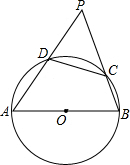 如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P
如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P
 如图,BD:DC=3:5,F是AD中点,那么S△AEF:S△FDC=3:13..
如图,BD:DC=3:5,F是AD中点,那么S△AEF:S△FDC=3:13..