��Ŀ����
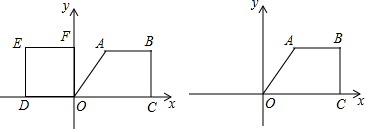
11����ͼ��ʾ����ƽ��ֱ������ϵ�У�ֱ������ABCO�ı�OC����x���ϣ���AB��OC��BC��OCAB=4��BC=6��OC=8��������ODEF�����߷ֱ������������ϣ��������������ֱ������ABCO���������������ODEF��x���������ƽ�ƣ����������ε��ص����ֵ����ΪS����1����������㣺��������ODEF�ı߳���
��2����������⣺
��������ODEFƽ�ƹ����У�ͨ���������۲죬���ж�S��S��0���ı仯�����C��
A�������� B������ C������������ D���ȼ��ٺ�����
�ڵ�������ODEF����O�ƶ�����Cʱ����S��ֵ��
��3��̽������ɣ�
��������ODEF����O�����ƶ��ľ���Ϊx�����ص��������S��x�ĺ�����ϵ��
���� ��1���������μ������ε������ʽ�����ǵ������ȣ�����������εı߳���
��2������ͼ�ε��ƶ���֪����OF�������ص��������������OF��BC�غ�ʱ���������ƶ�ʱ���������С�������ص��������ʱ���ɽ���ת��ΪS����AMDG+S����AGCB��
��3���������⽫ͼ��ƽ�ƣ������ƶ��ľ��벻ͬ����������ۣ��ص�����Ϊ�����Ρ�����κ;��Σ������������ε������ʽ�е�ʽ���ڸ������������ʽ�е�ʽ���ۢ����÷ָ������λ�Ϊ�����κ����ν�𣻢ݸ��ݾ��������ʽ���
��� �⣺��1����BC��OC��AB=4��BC=6��OC=8��
������ABCO�����=$\frac{1}{2}$��4+8����6=36��
�������ε��������ֱ������ABCO�������
��SODEF=SABCD=36��
�������εı߳�Ϊx��
��x2=36��
���x=6��x=-6����ȥ����
��������ODEF�ı߳�Ϊ6��
��2������ͼ�ɵã���������ODEF��x���������ƽ�ƣ��������ε��ص����ֵ�������������٣�
�ʴ�Ϊ��C��
����ͼ��ʾ����������ODEF����O�ƶ�����Cʱ��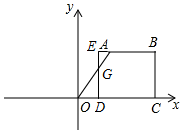
��AO��DE���ڵ�G��
��CD=6��OC=8��BE=6��AB=4��
��OD=8-6=2��AE=6-4=2��
��AE=OD��
�ڡ�AEG�͡�ODG�У�
$\left\{\begin{array}{l}{��E=��ODG}\\{��EGA=��DGO}\\{AE=OD}\end{array}\right.$��
���AEG�ա�ODG��AAS����
��EG=DG=$\frac{1}{2}$DE=3��
���AEG���=$\frac{1}{2}$AE��EG=$\frac{1}{2}$��2��3=3��
�������������ε��ص����ֵ����=36-3=33��
��S=33��
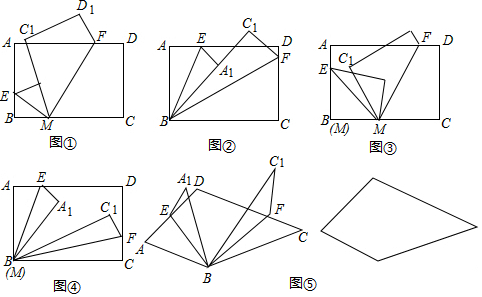
��3���ٵ�0��x��4ʱ���ص�����Ϊ�����Σ���ͼ�٣�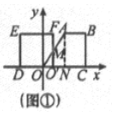
��ͼ�ɵá�OMO'�ס�OAN��
��$\frac{MO'}{6}$=$\frac{x}{4}$��
��MO'=$\frac{3}{2}$x��
��S=$\frac{1}{2}$OO'��MO'=$\frac{1}{2}$x��$\frac{3}{2}$x=$\frac{3}{4}{x}^{2}$��
�ڵ�4��x��6ʱ���ص�����Ϊֱ�����Σ���ͼ�ڣ�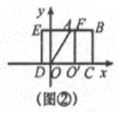
CO'=8-x��
S=36-��8-x����6=6x-12��
�۵�6��x��8ʱ���ص�����Ϊ����Σ���ͼ�ۣ�
OD=x-6��
��MD=$\frac{3}{2}$��x-6����AF=x-4��AE=6-��x-4����
��S=$\frac{1}{2}$[$\frac{3}{2}$��x-6��+6]��[6-��x-4��]+��x-4����6
=-$\frac{3}{4}$x2+15x-39��
�ܵ�8��x��10ʱ���ص�����Ϊ����Σ���ͼ�ܣ�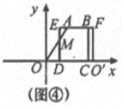
S=SAFO'DM-SBFO'C=$\frac{1}{2}$[��x-4��+x]��6-$\frac{1}{2}$����x-6����$\frac{3}{2}$��x-6��-��x-8����6=-$\frac{3}{4}$x2+9x+9��
�ݵ�10��x��14ʱ���ص�����Ϊ���Σ���ͼ�ݣ�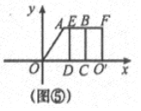
S=[8-��x-6��]��6=84-6x��
���� ���������ı����ۺ��⣬��Ҫ������ֱ�����Ρ������ε����ʣ����������ε��ж������ʣ�ȫ�������ε��ж��������Լ������ε�������ۺ�Ӧ�ã��������Ĺؼ����������⻭��ͼ�ν��з�������ۣ�

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д� ����ˬ��ͼ�����ĸ�ȫ�ȵ�ֱ�����������м�һ��С������ƴ�ɵĴ������Σ���ͼ����һ����ˬ��ͼ�����ڰ壬��ֱ�������ε�����ֱ�DZߵij��ֱ���2��4��С��ͬѧ����ڰ�һ����������ڰ�Ͷ�����ڣ�����Ͷ���ķ��ھ����ڷ��ڰ��ϣ�����Ͷ��һ�η��������м�С�������������ߣ��ĸ����ǣ�������
����ˬ��ͼ�����ĸ�ȫ�ȵ�ֱ�����������м�һ��С������ƴ�ɵĴ������Σ���ͼ����һ����ˬ��ͼ�����ڰ壬��ֱ�������ε�����ֱ�DZߵij��ֱ���2��4��С��ͬѧ����ڰ�һ����������ڰ�Ͷ�����ڣ�����Ͷ���ķ��ھ����ڷ��ڰ��ϣ�����Ͷ��һ�η��������м�С�������������ߣ��ĸ����ǣ�������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{2}{5}$ | D�� | $\frac{2}{3}$ |
| A�� | 20 | B�� | -20 | C�� | 28 | D�� | -2 |
| A�� | $\frac{2}{{\sqrt{2}}}$ | B�� | $\root{3}{2}$ | C�� | $\sqrt{0.5}$ | D�� | $\sqrt{8}$ |