Question

1．（1）填空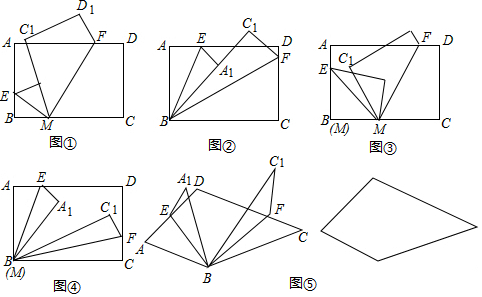

①把一张长方形的纸片按如图①所示的方式折叠，EM，FM为折痕，折叠后的C点落在B₁M或B₁M的延长线上，那么∠EMF的度数是90°；
②把一张长方形的纸片按如图②所示的方式折叠，B点与M点重合，EM，FM为折痕，折叠后的C点落在A₁M或A₁M的延长线上，那么∠EMF的度数是45°．
（2）解答
①把一张长方形的纸片按如图③所示的方式折叠，EM，FM为折痕，折叠后的C点落在B₁M或B₁M的延长线左侧，且∠EMF=80°，求∠C₁MB₁的度数；
②把一张长方形的纸片按如图④所示的方式折叠，B点与M点重合，EM，FM为折痕，折叠后的C点落在A₁M或A₁M的延长线右侧，且∠EMF=60°，求∠C₁MA₁的度数．
（3）探究
把一张四边形的纸片按如图⑤所示的方式折叠，EB，FB为折痕，设∠ABC=α°，∠EBF=β°，∠A₁BC₁=γ°，求α，β，γ之间的数量关系．

Answer 1

分析 （1）①如图①中，由∠EMF=∠EMC₁+∠C₁MF=$\frac{1}{2}$（∠BMC₁+∠C₁MC）=$\frac{1}{2}$×180°=90°，即可解决问题．②如图②中，由∠EBF=∠EBC₁+∠C₁BF=$\frac{1}{2}$（∠ABC₁+∠C₁BC）=$\frac{1}{2}$×90°=45°，即可解决问题．
（2）①如图③中，由折叠可知，∠CMF=∠FMC₁，∠BME=∠EMB₁，由∠C₁MF+∠EMB₁-∠EMF=∠C₁MB₁，推出∠CMF+∠BME-∠EMF=∠C₁MB₁，推出（∠BMC-∠EMF）-∠EMF=∠C₁MB₁，由此即可解决问题．②如图④中，根据折叠可知，∠CMF=∠C₁MF，∠ABE=∠A₁BE，由2∠CMF+2∠ABE+∠A₁MC₁=90°，推出2（∠CMF+∠ABE）+∠A₁MC₁=90°，推出2（90°-∠EMF）+∠A₁MC₁=90°，由此即可解决问题．
（3）如图中⑤-1中，由折叠可知，α-β=β-γ，推出α+γ=2β；如图⑤-2中，由折叠可知，α-β=β+γ，推出α-γ=2β，即可解决问题．

解答 解：（1）①如图①中，
∵∠EMC₁=$\frac{1}{2}$∠BMC₁，∠C₁MF=$\frac{1}{2}$∠C₁MC，
∴∠EMF=∠EMC₁+∠C₁MF=$\frac{1}{2}$（∠BMC₁+∠C₁MC）=$\frac{1}{2}$×180°=90°，
故答案为90°．

②如图②中，
∵∠EBA₁=$\frac{1}{2}$∠ABC₁，∠C₁BF=$\frac{1}{2}$∠C₁BC，
∴∠EBF=∠EBC₁+∠C₁BF=$\frac{1}{2}$（∠ABC₁+∠C₁BC）=$\frac{1}{2}$×90°=45°，
故答案为45°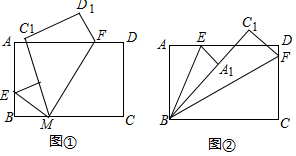


（2）①如图③中，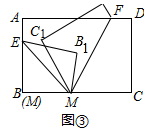

由折叠可知，∠CMF=∠FMC₁，∠BME=∠EMB₁，
∵∠C₁MF+∠EMB₁-∠EMF=∠C₁MB₁，
∴∠CMF+∠BME-∠EMF=∠C₁MB₁，
∴（∠BMC-∠EMF）-∠EMF=∠C₁MB₁，
∴180°-80°=∠C₁MB₁=20°．

②如图④中，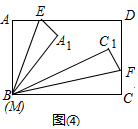

根据折叠可知，∠CMF=∠C₁MF，∠ABE=∠A₁BE，
∵2∠CMF+2∠ABE+∠A₁MC₁=90°，
∴2（∠CMF+∠ABE）+∠A₁MC₁=90°，
∴2（90°-∠EMF）+∠A₁MC₁=90°，
∴2（90°-60°）+∠A₁MC₁=90°，
∴∠A₁MC₁=30°．

（3）如图中⑤-1中，
由折叠可知，α-β=β-γ，
∴α+γ=2β．
如图⑤-2中，
由折叠可知，α-β=β+γ，
∴α-γ=2β．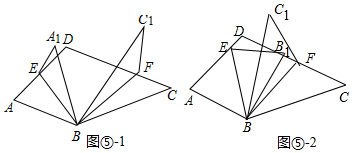

点评 本题考查几何变换综合题、矩形的性质、翻折不变性等知识，解题的关键是熟练掌握翻折不变性解决问题，灵活应用角的和差定义解决问题，属于中考常考题型．