题目内容
19.提出问题:以n边形的n个顶点和它内部的m个点,共(m+n)个点作为顶点,可把原n边形分割成多少个互不重叠的小三角形?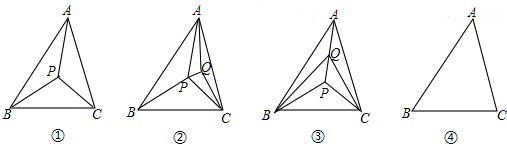
问题探究:为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:
探究一:以△ABC的3个顶点和它内部的1个点P,共4个点为顶点,可把△ABC分割成多少个互不重叠的小三角形?
如图①,显然,此时可把△ABC分割成3个互不重叠的小三角形.
探究二:以△ABC的3个顶点和它内部的2个点P、Q,共5个点为顶点,可把△ABC分割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①△ABC的内部,再添加1个点Q,那么点Q的位置会有两种情况:
第一种情况,点Q在图①分割成的某个小三角形内部.不妨设点Q在△PAC的内部,如图②;另一种情况,点Q在图①分割成的小三角形的某条公共边上.不妨设点Q在PA上,如图③.显然,不管哪种情况,都可把△ABC分割成5个互不重叠的小三角形.
探究三:以△ABC的三个顶点和它内部的3个点P、Q、R,共6个点为顶点,可把△ABC分割成7个互不重叠的小三角形,并在图④中画出一种分割示意图.
探究四:以△ABC的三个顶点和它内部的m个点,共(m+3)个点为顶点,可把△ABC分割成(2m+1)个互不重叠的小三角形.
探究拓展:以四边形的4个顶点和它内部的m个点,共(m+4)个点为顶点,可把四边形分割成(2m+2)个互不重叠的小三角形.
问题解决:以n边形的n个顶点和它内部的m个点,共(m+n)个点作为顶点,可把原n边形分割成(2m+n-2)个互不重叠的小三角形.
实际应用:以八边形的8个顶点和它内部的2012个点,共2020个顶点,可把八边形分割成多少个互不重叠的小三角形?(要求列式计算)
分析 探究三:分三角形内部三点共线与不共线两种情况作出分割示意图,查出分成的部分即可;
探究四:根据前三个探究不难发现,三角形内部每增加一个点,分割部分增加2部分,根据此规律写出(m+3)个点分割的部分数即可;
探究拓展:类似于三角形的推理写出规律整理即可得解;
问题解决:根据规律,把相应的点数换成m、n整理即可得解;
实际应用:把公式中的相应的字母,换成具体的数据,然后计算即可得解.
解答 解:探究三:分割示意图不唯一,如下图所示: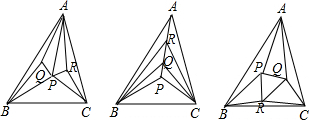
可把△ABC分割成7个互不重叠的小三角形,
故答案为:7;
探究四:三角形内部1个点时,共分割成3部分,3=3+2(1-1),
三角形内部2个点时,共分割成5部分,5=3+2(2-1),
三角形内部3个点时,共分割成7部分,7=3+2(3-1),
…,
所以,三角形内部有m个点时,3+2(m-1)=2m+1,
故答案为:(2m+1);
探究拓展:
四边形的4个顶点和它内部的m个点,
则分割成的不重叠的三角形的个数为:4+2(m-1)=2m+2,
故答案为:(2m+2);
问题解决:n+2(m-1)=2m+n-2,
故答案为:(2m+n-2);
实际应用:把n=8,m=2012代入上述代数式,得
2m+n-2,
=2×2012+8-2,
=4024+8-2,
=4030.
点评 本题考查了应用与设计作图,图形的变化规律的问题,读懂题目信息,根据前四个探究得到每多一个点,则三角形的个数增加2是解题的关键.

练习册系列答案
相关题目
9.“a与b的差的2倍”用代数式表示为( )
| A. | a-2b | B. | 2a-b | C. | 2(a-b) | D. | $\frac{a-b}{2}$ |
 如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论:
如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论: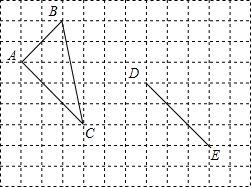 已知:如图所示的网格中有△ABC,
已知:如图所示的网格中有△ABC,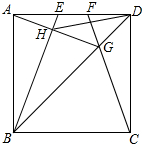 如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H. 如图,完成下列各题:
如图,完成下列各题: