题目内容
11.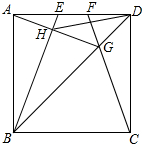 如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧的两个端点字母;
(3)直接写出线段DH长度的最小值.
分析 (1)根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠DAG=∠DCG,利用“边角边”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠DCF=∠ABE,从而证得∠DAG=∠ABE;
(2)①根据全等三角形对应角相等可得∠DCF=∠ABE,从而证得∠DAG=∠ABE,然后求出∠AHB=90°,再根据圆周角定理即可证得;
②以AB的中点O为圆心,OA长为半径画弧,交BD于I;
(3)根据直角三角形斜边上的中线等于斜边的一半,取AB的中点O,连接OH、OD,然后求出OH=$\frac{1}{2}$AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
解答  (1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
(1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAD=∠CDA=90°}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADG=∠CDG=45°}\\{DG=DG}\end{array}\right.$,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠DAG=∠ABE;
(2)①如图1,∵∠DAG=∠ABE,∠BAH+∠DAG=∠BAD=90°,
∴∠ABE+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG,
∴点H总在以AB为直径的圆弧上;
②如图2,以AB的中点O为圆心,OA长为半径画弧,交BD于I(I是BD的中点),弧的两个端点为A和I.
(3)如图3,取AB的中点O,连接OH、OD,
则OH=AO=$\frac{1}{2}$AB=2cm,
在Rt△AOD中,OD=$\sqrt{O{A}^{2}+A{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2$\sqrt{5}$-2.
点评 本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出DH最小时点H的位置是解题关键,也是本题的难点.

| A. | 9 | B. | 18 | C. | 10 | D. | 24 |
| A. | 三边的垂直平分线的交点 | B. | 三边上高的交点 | ||
| C. | 三边上中线的交点 | D. | 三内角平分线的交点 |
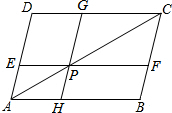 如图,在平行四边形ABCD中,EF∥AB,GH∥BC,EF、GH 交于点P,则图中除原来的平行四边形ABCD外,平行四边形的个数是( )
如图,在平行四边形ABCD中,EF∥AB,GH∥BC,EF、GH 交于点P,则图中除原来的平行四边形ABCD外,平行四边形的个数是( )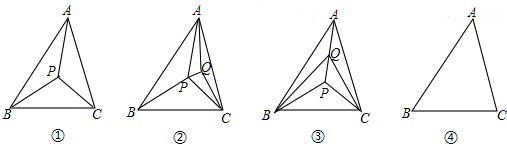
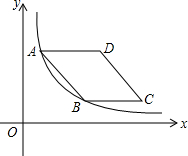 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.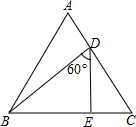 如图,△ABC为正三角形,D、E分别是AC、BC上的动点,当∠BDE=60°时,
如图,△ABC为正三角形,D、E分别是AC、BC上的动点,当∠BDE=60°时,