题目内容
10. 如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论:
如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论:①DN⊥MC;②DN垂直平分MC;③sin∠OCD=$\frac{12}{13}$;④S△ODC=S四边形BMON中,
正确的有①③④(填写序号)
分析 根据正方形的性质得出BC=CD,∠ABC=∠BCD=90°,然后根据SAS证得△BMC≌△CND,得出∠MCB=∠NDC.进而即可证得∠DOC=90°,即DN⊥MC;根据勾股定理求得DN,然后根据$\frac{1}{2}$NC•CD=$\frac{1}{2}$ND•OC,求得OC=$\frac{60}{13}$,OM=13-$\frac{60}{13}$=$\frac{109}{13}$,则OC≠OM,因为∠DNC+∠NDC=90°,∠ODC+∠OCD=90°,得出∠OCD=∠DNC,所以sin∠OCD=sin∠DNC=$\frac{CD}{DN}$=$\frac{12}{13}$;由△BMC≌△CND,得出S△BMC=S△CND,求得S△BMC-S△CNC=S△CND-S△CNC,即S四边形BMON=S△ODC.
解答 解:∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠BCD=90°,
在△BMC和△CND中,
$\left\{\begin{array}{l}{BC=CD}\\{∠ABC=∠BCD}\\{BM=CN}\end{array}\right.$,
∴△BMC≌△CND,
∴∠MCB=∠NDC.
又∠MCN+∠MCD=90°,
∴∠MCD+∠NDC=90°,
∴∠DOC=90°,
∴DN⊥MC,故①正确;
在Rt△CDN中,∵CD=12,CN=5,
∴DN=$\sqrt{{CD}^{2}+C{N}^{2}}$=13.
又∵∠BCD=90°,∠COD=90°
∴$\frac{1}{2}$NC•CD=$\frac{1}{2}$ND•OC,
∴OC=$\frac{60}{13}$,OM=13-$\frac{60}{13}$=$\frac{109}{13}$,
∴OC≠OM,故②错误;
∵∠DNC+∠NDC=90°,∠ODC+∠OCD=90°,
∴∠OCD=∠DNC,
∴sin∠OCD=sin∠DNC=$\frac{CD}{DN}$=$\frac{12}{13}$,故③正确;
∵△BMC≌△CND,
∴S△BMC=S△CND
S△BMC-S△CNC=S△CND-S△CNC,即S四边形BMON=S△ODC,故④正确.
综上,正确的结论是①③④.
故答案为①③④.
点评 本题考查了正方形的性质,三角形全等的判定和性质,勾股定理的应用,解直角三角形以及三角形面积等,熟练掌握待定系数法是解题的关键.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案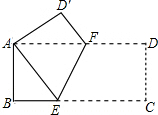 如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 8$\sqrt{5}$cm | D. | 16cm |
| A. | 三边的垂直平分线的交点 | B. | 三边上高的交点 | ||
| C. | 三边上中线的交点 | D. | 三内角平分线的交点 |
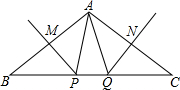 如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°,则∠PAQ等于20°,若BC=10,则△PAQ的周长等于10.
如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°,则∠PAQ等于20°,若BC=10,则△PAQ的周长等于10.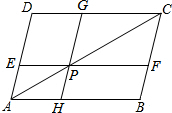 如图,在平行四边形ABCD中,EF∥AB,GH∥BC,EF、GH 交于点P,则图中除原来的平行四边形ABCD外,平行四边形的个数是( )
如图,在平行四边形ABCD中,EF∥AB,GH∥BC,EF、GH 交于点P,则图中除原来的平行四边形ABCD外,平行四边形的个数是( ) 如图,已知点I是△ABC的内心,AI交BC于D,交外接圆O于E,求证:
如图,已知点I是△ABC的内心,AI交BC于D,交外接圆O于E,求证: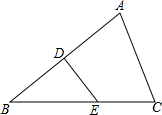 △ABC中,AB=BC,DE是AB的中垂线,BE=AC,求∠ACB的度数.
△ABC中,AB=BC,DE是AB的中垂线,BE=AC,求∠ACB的度数.