题目内容
7.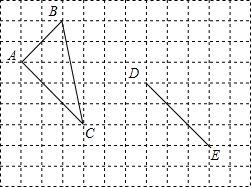 已知:如图所示的网格中有△ABC,
已知:如图所示的网格中有△ABC,(1)请你画出所有满足条件的△DEF,使△ABC与△DFE全等;
(2)计算△ABC的面积.
分析 (1)直接利用网格,结合全等三角形的判定方法得出符合题意的图形;
(2)利用勾股定理的逆定理得出△ABC是直角三角形,进而求出其面积.
解答 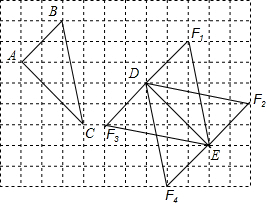 解:(1)如图所示:
解:(1)如图所示:
△DF1E,△DF2E,△DF3E,△DF4E,都与△ABC全等;
(2)∵AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
BC=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴△ABC的面积为:$\frac{1}{2}$×2$\sqrt{2}$×3$\sqrt{2}$=6.
点评 此题主要考查了复杂作图以及全等三角形的判定和三角形面积求法,正确利用勾股定理逆定理是解题关键.

练习册系列答案
相关题目
18.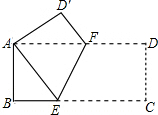 如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
 如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 8$\sqrt{5}$cm | D. | 16cm |
12.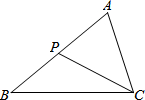 如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )
如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )
 如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )
如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{PC}{BC}$=$\frac{AC}{AB}$ | D. | $\frac{AC}{AB}$=$\frac{AP}{AC}$ |
17.若9x2+mxy+16y2是一个完全平方式,那m的值是( )
| A. | ±12 | B. | -12 | C. | ±24 | D. | -24 |
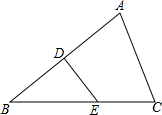 △ABC中,AB=BC,DE是AB的中垂线,BE=AC,求∠ACB的度数.
△ABC中,AB=BC,DE是AB的中垂线,BE=AC,求∠ACB的度数.
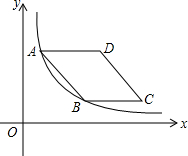 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.