题目内容
8.已知△ABC∽△A′B′C′,AB=2,A′B′=3,那么它们的面积之比为4:9.分析 根据相似三角形的面积的比等于相似比的平方进行解答.
解答 解:∵$\frac{AB}{A′B′}$=$\frac{2}{3}$,
∴△ABC和△A′B′C′的相似比是$\frac{2}{3}$,
∴它们的面积之比为$\frac{4}{9}$,
故答案为:$\frac{4}{9}$.
点评 本题考查的是相似三角形的性质,掌握相似三角形的面积的比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
18.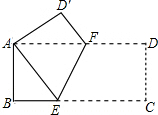 如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
 如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )
如图所示,矩形纸片ABCD中,AD=2AB,现将其沿EF折叠,使得点C与点A重合,若AF=10cm,则折痕EF的长为( )| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 8$\sqrt{5}$cm | D. | 16cm |
3.在Rt△ABC中,斜边AB=3,则AB2+AC2+BC2=( )
| A. | 9 | B. | 18 | C. | 10 | D. | 24 |
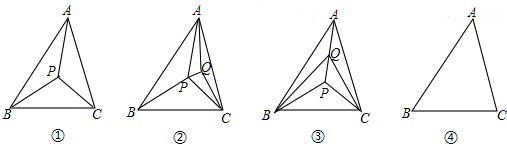
20.到三角形三边距离相等的点是( )
| A. | 三边的垂直平分线的交点 | B. | 三边上高的交点 | ||
| C. | 三边上中线的交点 | D. | 三内角平分线的交点 |
17.若9x2+mxy+16y2是一个完全平方式,那m的值是( )
| A. | ±12 | B. | -12 | C. | ±24 | D. | -24 |
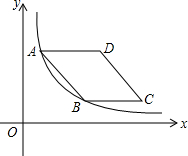 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.