题目内容
7.若a>2b>0,a2+4b2-8ab=0,则$\frac{2b+a}{2b-a}$=-$\sqrt{3}$.分析 根据题意、结合完全平方公式和算术平方根的性质求出a+2b和a-2b的值,代入所求的式子计算即可.
解答 解:∵a2+4b2-8ab=0,
∴a2+4ab+4b2-12ab=0,
即(a+2b)2=12ab,
∵a>2b>0,
∴a+2b=2$\sqrt{3ab}$,
∵a2+4b2-8ab=0,
∴a2-4ab+4b2-4ab=0,
即(a-2b)2=4ab,又a>2b>0,
∴a-2b=2$\sqrt{ab}$,
∴$\frac{2b+a}{2b-a}$=$\frac{2\sqrt{3ab}}{-2\sqrt{ab}}$=-$\sqrt{3}$,
故答案为:-$\sqrt{3}$.
点评 本题考查的是完全平方公式的应用,熟练运用完全平方公式:(a±b)2=a2±2ab+b2是解题的关键,注意算术平方根的应用.

练习册系列答案
相关题目
17.已知a是关于x的方程2(x+$\frac{4}{13}$)=$\frac{2}{7}$的解,则3-(a+$\frac{4}{13}$)的值为( )
| A. | 3$\frac{1}{7}$ | B. | 2$\frac{6}{7}$ | C. | -$\frac{6}{7}$ | D. | -2$\frac{6}{7}$ |
 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.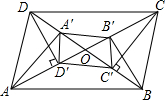 已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).
已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).