题目内容
12.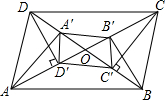 已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).
已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).(1)试说明:四边形A′B′C′D′∽?ABCD;
(2)四边形A′B′C′D′与?ABCD是不是位似图形.
分析 (1)根据垂直的定义得到∠AA’D=∠AD’D=90°,得到A、D’、A’、D四点共圆,证明OAD∽△OA’D’,根据相似三角形的性质证明$\frac{AD}{A′D′}$=$\frac{CD}{C′D′}$,∠ADC=∠A’D’C’,证明结论;
(2)根据位似图形的对应边互相平行进行判断即可.
解答 证明:(1)∵∠AA’D=∠AD’D=90°,
∴A、D’、A’、D四点共圆,
∴∠DAA’=∠DD’A’,
∵∠ODA=90°-∠DAA’,∠OD’A’=90°-∠DD’A(直角三角形的锐角互补)
所以:∠ODA=∠OD’A’,
∴OAD∽△OA’D’,
∴$\frac{AD}{A′D′}$=$\frac{OD}{OD′}$,∠OAD=∠OA’D′,
同理可证:$\frac{CD}{A′B′}$=$\frac{OD}{OB′}$,∠ODC=∠OB’A’,
∵C’D’=A’B’,OB’=OD’,
∴$\frac{CD}{C′D′}$=$\frac{OD}{OD′}$,
∴$\frac{AD}{A′D′}$=$\frac{CD}{C′D′}$,
同理可证:∠OD’C′=∠OBA,
∵AB∥CD,
∴∠OBA=∠ODC,
∴∠OD’C=∠ODC,
∴∠ADC=∠ODA+∠ODC=∠OD’A+∠OD’C=∠A’D’C’,
∴平行四边形ABCD∽平行四边形A’B’C’D’相似;
(2)∵AD与A′D′不平行,
∴四边形A′B′C′D′与?ABCD不是位似图形.
点评 本题考查的是位似变换和相似三角形的性质,掌握位似变换的概念和相似三角形对应边成比例,对应角相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法中正确的有( )
①弧可分为优弧和劣弧;
②长度相等的两条弧是等弧;
③经过圆心的每一条直线都是圆的对称轴;
④直径是弦.
①弧可分为优弧和劣弧;
②长度相等的两条弧是等弧;
③经过圆心的每一条直线都是圆的对称轴;
④直径是弦.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
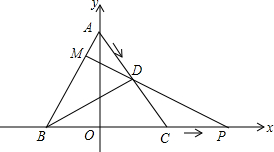 如图,将等边三角形ABC放在平面直角坐标系中,使得BC在x轴上,点A在y轴正半轴上,已知AB=4,AO=2$\sqrt{3}$,若点D从A出发沿AC向C运动,点P从C出发沿x轴正方向运动,点D、P均以每秒0.5个单位长度的速度同时开始运动,设运动时间为t,运动过程中连接PD并延长交AB于点M.
如图,将等边三角形ABC放在平面直角坐标系中,使得BC在x轴上,点A在y轴正半轴上,已知AB=4,AO=2$\sqrt{3}$,若点D从A出发沿AC向C运动,点P从C出发沿x轴正方向运动,点D、P均以每秒0.5个单位长度的速度同时开始运动,设运动时间为t,运动过程中连接PD并延长交AB于点M. 如图,在△ABC中,AB>AC>BC,∠ACB=80°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数.
如图,在△ABC中,AB>AC>BC,∠ACB=80°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数.