题目内容
19.小明从甲地去往乙地,如果按照原计划的速度走12公里,然后将速度提高30%,那么将提前1小时到达乙地.如果按照原计划走1小时20分,然后将速度提高25%.那么也可以提前1小时到达乙地,则甲、乙两地之间的距离是38公里.分析 设甲、乙两地之间的距离为x公里,小明原计划的速度是a公里/小时.根据题意列出方程组,解方程组即可,注意要验根.
解答 解:设甲、乙两地之间的距离为x公里,小明原计划的速度是a公里/小时;
根据题意得:$\left\{\begin{array}{l}{\frac{12}{a}+\frac{x-12}{1.3a}=\frac{x}{a}-1}\\{\frac{4}{3}+\frac{x-\frac{4}{3}a}{\frac{\frac{5}{4}a}{\;}}=\frac{x}{a}-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=6}\\{x=38}\end{array}\right.$,
经检验,a=6,x=38时所列方程组的解;
即甲、乙两地之间的距离为38公里.
故答案为:38.
点评 本题考查了列分式方程组解应用题;根据题意设出两个未知数,由时间关系列出方程组是解决问题的关键.

练习册系列答案
相关题目
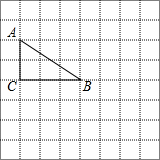 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都在格点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都在格点上. 如图,在△ABC中,AB>AC>BC,∠ACB=80°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数.
如图,在△ABC中,AB>AC>BC,∠ACB=80°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数.