题目内容
13. 如图,平行四边形ABCD内接于⊙O,则∠ADC=( )
如图,平行四边形ABCD内接于⊙O,则∠ADC=( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
分析 根据平行四边形的性质得到∠ABC=∠AOC,根据圆内接四边形的性质、圆周角定理列式计算即可.
解答 解:∵四边形ABCD是平行四边形,
∴∠ABC=∠AOC,
∵平行四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=180°,
由圆周角定理得,∠ADC=$\frac{1}{2}$∠AOC,
∴∠ADC=60°,
故选:C.
点评 本题考查的是圆内接四边形的性质、圆周角定理以及平行四边形的性质,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
相关题目
4.已知1微米=10-7米,则25微米用科学记数法表示为( )
| A. | 0.25×10-5米 | B. | 25×10-7米 | C. | 2.5×10-6米 | D. | 2.5×10-8米 |
18.下列图形,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.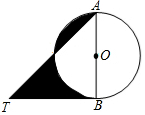 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )| A. | 2 | B. | $\frac{3}{2}$-$\frac{1}{4}$π | C. | 1 | D. | $\frac{1}{2}$+$\frac{1}{4}$π |
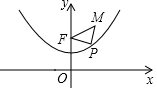 已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )
已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( ) 如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为$\sqrt{3}$,弦CD的长为3cm,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{4}$..
如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为$\sqrt{3}$,弦CD的长为3cm,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{4}$..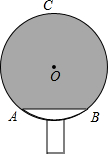 如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.
如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.