题目内容
5.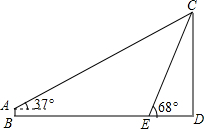 如图,条幅从楼顶C处拉下,在E处固定,条幅CE与地面成68°角,在离楼底D点40米处安置测角仪AB,在A处测得点C的仰角为37°.已知测角仪的高为1.5米,求条幅的长度(结果保留整数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,条幅从楼顶C处拉下,在E处固定,条幅CE与地面成68°角,在离楼底D点40米处安置测角仪AB,在A处测得点C的仰角为37°.已知测角仪的高为1.5米,求条幅的长度(结果保留整数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
解答 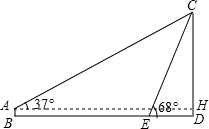 解:过点A作AH⊥CD,垂足为H,
解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=37°,
则AB=DH=1.5米,BD=AH=40米,
∵在Rt△ACH中,tan∠CAH=$\frac{CH}{AH}$,
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=40•tan37°≈40×0.75=30(米),
∵DH=1.5米,
∴CD≈30+1.5=31.5,
在Rt△CDE中,∵∠CED=60°,sin∠CED=$\frac{CD}{CE}$,
∴CE=$\frac{CD}{sin68°}$≈$\frac{31.5}{0.93}$≈34(米),
答:条幅的长约为34米.
点评 此题主要考查解直角三角形的应用-仰角俯角问题.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
20.我们学习了圆周角定理,回顾学习过程,在探索同弧所对的圆周角和圆心角的关系时,主要体现的数学思想是( )
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |
17.已知P(2t+1,3t-2)是第四象限内的整点(模拟坐标都为整数的点称为整点),则P的坐标为( )
| A. | (1,-2) | B. | (1,2) | C. | (-2,-1) | D. | (2,-1) |
 已知A、B、C在一直线上,X、Y、Z在一直线上,并且AY∥BZ,BX∥CY,求证:AX∥CZ.
已知A、B、C在一直线上,X、Y、Z在一直线上,并且AY∥BZ,BX∥CY,求证:AX∥CZ.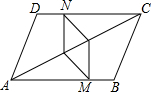 如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.
如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.