题目内容
15．
已知A、B、C在一直线上，X、Y、Z在一直线上，并且AY∥BZ，BX∥CY，求证：AX∥CZ．
分析 根据同底等高的三角形的面积相等，由BX∥CY得到S△BXC=S△BXY，AY∥BZ得到S△AYZ=S△ABY，再利用面积的变换可得S△AXC=S△AXZ=S四边形AXYB，于是可判断点C和点Z到AX的距离相等，所以AX∥CZ．
解答 解：连结AC、AZ、BY，如图，
S△AXC=S△AXB+S△BXC，
∵BX∥CY，
∴S△BXC=S△BXY，
∴S△AXC=S△AXB+S△BXY=S四边形AXYB，
S△AXZ=S△AXY+S△AYZ，
∵AY∥BZ，
∴S△AYZ=S△ABY，
∴S△AXZ=S△AXY+S△ABY=S四边形AXYB，
∴S△AXC=S△AXZ，
∴AX∥CZ．
点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．也考查了同底等高的三角形的面积相等．
练习册系列答案
相关题目
5．若-4x2y和-2xmyn是同类项，则m，n的值分别是（ ）
| A． | m=2，n=1 | B． | m=2，n=0 | C． | m=4，n=1 | D． | m=4，n=0 |
6．如果$\sqrt{x+2}$=2，那么x等于（ ）
| A． | 16 | B． | 8 | C． | 4 | D． | 2 |
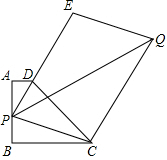已知梯形ABCD中，AD∥BC，∠B=90°，AD=1，AB=3，BC=4．若P为线段AB上任意一点，延长PD到E，使DE=2PD，以PE、PC为边作?PCQE，则对角线PQ的最小值为7．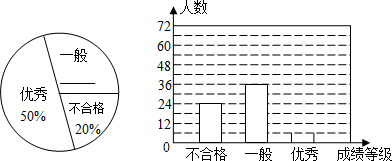
如图，D为圆O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40%．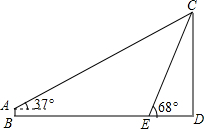
如图，条幅从楼顶C处拉下，在E处固定，条幅CE与地面成68°角，在离楼底D点40米处安置测角仪AB，在A处测得点C的仰角为37°．已知测角仪的高为1.5米，求条幅的长度（结果保留整数，参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）