题目内容
16.计算:$\left\{\begin{array}{l}{2x+y=-1}\\{{x}^{2}-3x-y-3=0}\end{array}\right.$.分析 把方程①化为y=-2x-1,代入②,得到关于x的一元二次方程,解方程求出x的值,然后求出y的值,得到方程组的解.
解答 解:$\left\{\begin{array}{l}{2x+y=-1①}\\{{x}^{2}-3x-y-3=0②}\end{array}\right.$
由①得,y=-2x-1③
把③代入②得,
x2-x-2=0
x1=-1,x2=2
把x1=-1,x2=2代入①得,
y1=1,y2=-5
所以方程组的解为$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-5}\end{array}\right.$
点评 本题考查的是二元二次方程组的解法,正确运用代入法是解题的关键,变形其中一个方程,用一个未知数表示另一个未知数,实现消元,求出方程组的解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
6.如果$\sqrt{x+2}$=2,那么x等于( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
 如图,D为圆O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为圆O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40%.
某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40%.
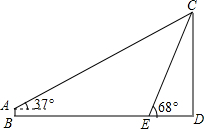 如图,条幅从楼顶C处拉下,在E处固定,条幅CE与地面成68°角,在离楼底D点40米处安置测角仪AB,在A处测得点C的仰角为37°.已知测角仪的高为1.5米,求条幅的长度(结果保留整数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,条幅从楼顶C处拉下,在E处固定,条幅CE与地面成68°角,在离楼底D点40米处安置测角仪AB,在A处测得点C的仰角为37°.已知测角仪的高为1.5米,求条幅的长度(结果保留整数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)