题目内容
10.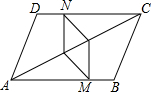 如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.
如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.
分析 四边形中若是一组对边平行且相等,那么这个四边形是平行四边形,根据题目所给的条件可证明一组对边平行相等就可以.
解答  证明:在?ABCD中,
证明:在?ABCD中,
∵AB∥CD,
∴∠BAC=∠DCA,
在△AME与△CNF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠BAC=∠DCA}\\{CN=AM}\end{array}\right.$,
∴△AME≌CNF,
∴EM=FN,∠AEM=∠CFN,
∴∠FEM=∠NFE,
∴EM∥FN,
∴四边形MENF是平行四边形.
点评 本题考查了平行四边形的判定和性质,以及全等三角形的判定和性质定理,熟记这些定理才能够准确运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
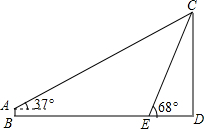 如图,条幅从楼顶C处拉下,在E处固定,条幅CE与地面成68°角,在离楼底D点40米处安置测角仪AB,在A处测得点C的仰角为37°.已知测角仪的高为1.5米,求条幅的长度(结果保留整数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,条幅从楼顶C处拉下,在E处固定,条幅CE与地面成68°角,在离楼底D点40米处安置测角仪AB,在A处测得点C的仰角为37°.已知测角仪的高为1.5米,求条幅的长度(结果保留整数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,若AD⊥BD,问四边形BEDF是什么特殊的四边形?
如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,若AD⊥BD,问四边形BEDF是什么特殊的四边形?