题目内容
5. 在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=45°.
在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=45°.
分析 作DH⊥BC于H,如图,易得四边形ABHD为矩形,则BH=AD=1,AB=DH,所以HC=BC-BH=1,再根据旋转的性质得∠FBD=90°,BF=BD,则可判断△BDF为等腰直角三角形,所以BA⊥DF,根据等腰直角三角形的性质得AB=AF=AD=1,则DH=1,然后再判断△DHC为等腰直角三角形,于是可得∠C=45°.
解答 解:作DH⊥BC于H,如图,
∵AD∥BC,∠DAB=90°,
∴四边形ABHD为矩形,
∴BH=AD=1,AB=DH,
∴HC=BC-BH=2-1=1,
∵△ABD绕着点B逆时针旋转90°得到△EBF,
∴∠FBD=90°,BF=BD,
∴△BDF为等腰直角三角形,
∵点F刚好落在DA的延长线上,
∴BA⊥DF,
∴AB=AF=AD=1,
∴DH=1,
∴△DHC为等腰直角三角形,
∴∠C=45°.
故答案为45°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
13.昌吉赣客运专线是我省第一条南北纵向的高速铁路,设计时速为每小时350公里,总投资约46200000000元.数字46200000000可用科学记数法表示为( )
| A. | 46.2×1010 | B. | 4.62×1011 | C. | 4.62×1010 | D. | 0.462×1011 |
17.若方程组$\left\{\begin{array}{l}x+2y=7+k\\ 5x-y=k\end{array}\right.$的解x与y是互为相反数,则k的值为( )
| A. | 4 | B. | 6 | C. | -6 | D. | -1 |
15.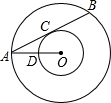 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 12 | B. | 6$\sqrt{3}$ | C. | 8 | D. | 3$\sqrt{3}$ |
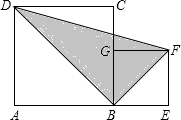 如图,正方形ABCD和正方形BEFG两正方形的面积分别是10和3,那么阴影部分面积是$\sqrt{30}$.
如图,正方形ABCD和正方形BEFG两正方形的面积分别是10和3,那么阴影部分面积是$\sqrt{30}$.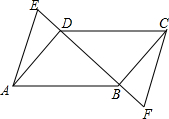 已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.
已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.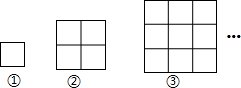 如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图象含有正方形的个数是( )
如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图象含有正方形的个数是( )