题目内容
6. 已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.
已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
分析 (1)利用已知得出Rt△BOC∽Rt△COA,进而得出∠OCA+∠OCB=90°,即可得出答案;
(2)由题意可得,方程-x2+ax+b=0有两个不同的实数根,进而得出C点坐标,可得出b的值,再利用tanα=$\frac{OB}{OC}$,tanβ=$\frac{OA}{OC}$,由tanα-tanβ=2,得出a的值进而得出答案;
(3)作PF⊥x轴于点F,根据S四边形ABPC=S△PDB-S△CDA=$\frac{1}{2}$DB•PF-$\frac{1}{2}$DA•OC,进而得出答案.
解答 解:(1)△ABC是直角三角形.
理由如下:
∵OC2=OA•OB,
∴$\frac{OC}{OB}$=$\frac{OA}{OC}$,
又∵∠BOC=∠COA=90°,
∴Rt△BOC∽Rt△COA,
∴∠OCB=∠OAC;
又∵∠OCA+∠OAC=90°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°,
∴△ABC是直角三角形;
(2)∵抛物线与x轴交于A、B两点,
∴方程-x2+ax+b=0有两个不同的实数根.
设这两个根分别为x1、x2,且x1<x2,
显然,x1<0,x2>0,
得A、B两点的坐标分别为A(x1,0)、B(x2,0).
由根与系数的关系,有x1+x2=a,x1•x2=-b.
对于抛物线y=-x2+ax+b,当x=0时,y=b,
∴C点的坐标为C(0,b);
由已知条件OC2=OA•OB,
得b2=(-x1)•x2,即b2=-x1•x2,
∴b2=b,
∵点C在y轴的正半轴上,
∴b>0,从而得b=1.
∵tanα=$\frac{OB}{OC}$,tanβ=$\frac{OA}{OC}$,
由tanα-tanβ=2,得$\frac{OB}{OC}$-$\frac{OA}{OC}$=2,即
OB-OA=2OC,
得x2-(-x1)=2b,x2+x1=2b,
即a=2b,
∴a=2.
∴抛物线的解析式为:y=-x2+2x+1;
(3)由抛物线的解析式y=-x2+2x+1
配方得:y=-(x-1)2+2,
∴其顶点P的坐标为P(1,2).
解方程-x2+2x+1=0,
得x1=1-$\sqrt{2}$,x2=1+$\sqrt{2}$,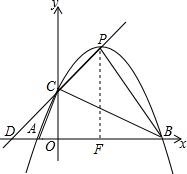
∴A(1-$\sqrt{2}$,0),B(1+$\sqrt{2}$,0).
解法一:设过P、C两点的直线与x轴交于点D,
直线的解析式为:y=kx+1,
把P(1,2)坐标代入,得k=1,
∴直线PC:y=x+1,当y=0时,x=-1,
即点D的坐标为D(-1,0).
∵-1<1-$\sqrt{2}$,
∴点D在点A的左边,
作PF⊥x轴于点F,
∴S四边形ABPC=S△PDB-S△CDA=$\frac{1}{2}$DB•PF-$\frac{1}{2}$DA•OC
=$\frac{1}{2}$[(1+$\sqrt{2}$)+1]×2-$\frac{1}{2}$[(1-$\sqrt{2}$)+1]×1
=$\frac{2+3\sqrt{2}}{2}$,
即四边形ABPC的面积为$\frac{2+3\sqrt{2}}{2}$.
解法二:过点P作PF⊥x轴于点F,
则∴S四边形ABPC=S△OAC+S梯形COFP+S△PFB
=$\frac{1}{2}$OA•OC+$\frac{1}{2}$(OC+PF)•OF+$\frac{1}{2}$FB•PF,
=$\frac{1}{2}$($\sqrt{2}$-1)×1+$\frac{1}{2}$(1+2)×1+$\frac{1}{2}$(1+$\sqrt{2}$-1)×2
=$\frac{2+3\sqrt{2}}{2}$;
即四边形ABPC的面积为$\frac{2+3\sqrt{2}}{2}$.
点评 此题主要考查了二次函数综合以及四边形面积求法和根与系数的关系以及相似三角形的判定与性质等知识,正确利用已知OC2=OA•OB,得出b的值是解题关键.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | x2÷x2=1 | B. | (-a2b)3=a6b3 | C. | (-3x)0=-1 | D. | (x+3)2=x2+9 |
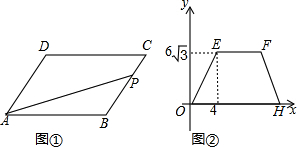
| A. | 11 | B. | 14 | C. | 8+$\frac{3}{2}\sqrt{3}$ | D. | 8+3$\sqrt{3}$ |
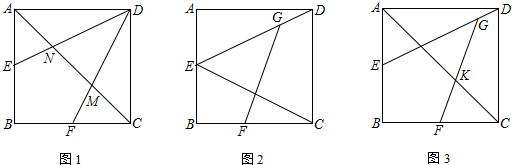
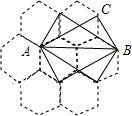 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.


