题目内容
18.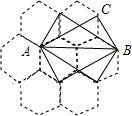 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.
分析 分类探究,如图数一下和线段AB、A′B′,A″B″类似的线段有多少,分别计算出和△ABC全等的三角形有多少即可解决问题.
解答 解:如图 类似于AB这样的线段有12条,共有12×4=48个三角形和△ABC全等,
类似于AB这样的线段有12条,共有12×4=48个三角形和△ABC全等,
类似于A′B′这样的线段有6条,共有6×2=12个三角形和△ABC全等,
类似于A″B″这样的线段有6条,共有6×4=24个三角形和△ABC全等,
一共有48+12+24=84个三角形和△ABC全等.
故答案为84.
点评 本题考查全等三角形的判定、解题的关键是学会讨论的思想,和线段AB相等的线段分成3类,这样就容易统计,掌握这种统计方法,属于中考填空题中的压轴题.

练习册系列答案
相关题目
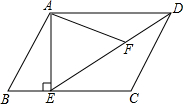 如图,在平行四边形ABCD中,过点A作AE⊥BE,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BE,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. 已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.
已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.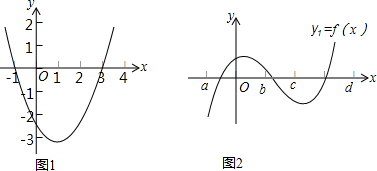
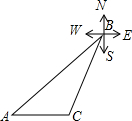 如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)
如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)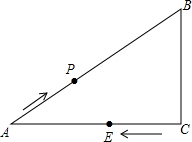 如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
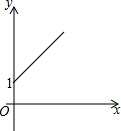
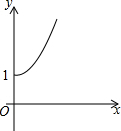
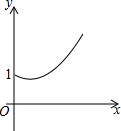
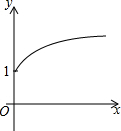
如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢? 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )