题目内容
16．已知抛物线y=ax2+bx+c的形状与抛物线y=x2的形状相同，最高点坐标为（2，-3），则抛物线的解析式是y=-x2+4x-7．分析 根据y=ax2+bx+c的形状与y=x2形状相同，且有最高点，可确定函数图象开口向下，且a=-1，由顶点坐标写出其顶点式，再整理成一般式即可．
解答 解：∵y=ax2+bx+c的形状与y=x2形状相同，且有最高点（2，-3），
∴抛物线的解析式是y=-（x-2）2-3=-x2+4x-7，
故答案为：y=-x2+4x-7．
点评 本题考查了待定系数法求函数解析式．掌握当|a|相等时两抛物线形状相同及抛物线顶点式是关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
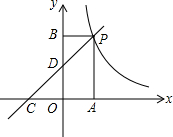如图，一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P，点P在第一象限，PA⊥x轴于点A，PB⊥y轴于点B，一次函数的图象分别交x轴、y轴于点C、D，S△PBD=2，OA=OC．求：
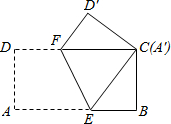如图，将长为4cm，宽为2cm的矩形纸片ABCD沿着EF翻叠，使点A与C重合，则折痕EF的长为$\sqrt{5}$cm．
1．由10个非负整数构成的一组数据x1，x2，…，x10．当它们的平均数、众数、中位数满足下列选项中的哪个时，可以保证x1，x2，…，x10中最大的数据一定不超过7．（ ）
| A． | 平均数为2，众数为2，中位数为2 | B． | 平均数为3，众数为2，中位数为4 | ||
| C． | 平均数为2，众数为3，中位数为2 | D． | 平均数为2，众数为3，中位数为4 |
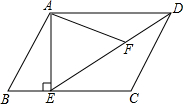如图，在平行四边形ABCD中，过点A作AE⊥BE，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．
已知，如图，抛物线y=-x2+ax+b与x轴从左至右交于A、B两点，与y轴正半轴交于点C．设∠OCB=α，∠OCA=β，且tanα-tanβ=2，OC2=OA•OB．