题目内容
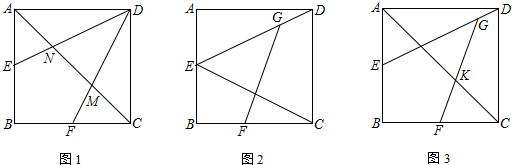
11.已知正方形ABCD中,E、F分别是AB、BC的中点,AB=4.(1)如图1,DE、DF分别交AC于N、M两点,直接写出$\frac{EN}{DN}$=$\frac{1}{2}$,MN=$\frac{4\sqrt{2}}{3}$;
(2)G是DE上一点,且∠EGF=45°;
①如图2,求GF的长;
②如图3,连接AC交GF于点K,求KF的长.
分析 (1)过点E作EG∥BC交AC于G,根据三角形中位线定理得到EG=$\frac{1}{2}$BC,根据平行线的性质求出$\frac{EN}{DN}$,根据勾股定理求出AG,计算即可;
(2)①连接AF,交ED于H,证明△DAE≌△ABF,得到△HFG为等腰直角三角形,根据等腰直角三角形的性质计算即可;
②连接EF、AF,由(1)(2)的结论得到AH=$\frac{4}{5}$$\sqrt{5}$,EH=$\frac{2\sqrt{5}}{5}$,AN=$\frac{4\sqrt{2}}{3}$,HN=$\frac{4\sqrt{5}}{15}$,根据平行线的性质计算即可.
解答 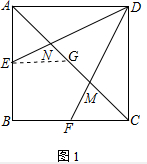 解:(1)如图1,过点E作EG∥BC交AC于G,
解:(1)如图1,过点E作EG∥BC交AC于G,
∵E是AB的中点,
∴EG=$\frac{1}{2}$BC=$\frac{1}{2}$AD=2,
∵EG∥BC,
∴$\frac{EN}{DN}$=$\frac{NG}{AN}$=$\frac{EG}{AD}$=$\frac{1}{2}$,
∵EA=EG=2,
∴AG=$\sqrt{E{A}^{2}+E{G}^{2}}$=2$\sqrt{2}$,
∴NG=$\frac{2\sqrt{2}}{3}$,
同理,GM=$\frac{2\sqrt{2}}{3}$,
∴MN=NG+MG=$\frac{4\sqrt{2}}{3}$,
故答案为:$\frac{1}{2}$;$\frac{4\sqrt{2}}{3}$;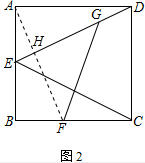
(2)如图2,连接AF,交ED于H,
在△DAE和△ABF中,
$\left\{\begin{array}{l}{DA=AB}\\{∠DAE=∠ABF}\\{AE=BF}\end{array}\right.$,
∴△DAE≌△ABF,
∴∠ADE=∠BAF,
∴AH⊥DE,
∵BF=2,AB=4,
∴AF=DE=2$\sqrt{5}$,
∴AH=$\frac{4}{5}$$\sqrt{5}$,HF=$\frac{6}{5}$$\sqrt{5}$,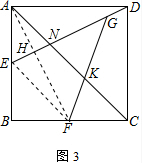
∵∠EGF=45°,
∴△HFG为等腰直角三角形,
∴GF=$\sqrt{2}$HF=$\frac{6}{5}$$\sqrt{10}$;
(3)如图3,连接EF、AF,
∵EF为△ABC的中位线,
∴EF∥AC,
由(1)(2)可知:AH=$\frac{4}{5}$$\sqrt{5}$,EH=$\frac{2\sqrt{5}}{5}$,AN=$\frac{4\sqrt{2}}{3}$,HN=$\frac{4\sqrt{5}}{15}$,
HG=HF=$\frac{6}{5}$$\sqrt{5}$,
∴NG=$\frac{6}{5}$$\sqrt{5}$-$\frac{4}{15}$$\sqrt{5}$=$\frac{14}{15}$$\sqrt{5}$,EN=EH+NH=$\frac{2}{3}$$\sqrt{5}$,
∴$\frac{GK}{KF}$=$\frac{GN}{NE}$=$\frac{7}{5}$,
∴KF=$\frac{1}{2}$$\sqrt{10}$.
点评 本题考查的是正方形的性质、等腰直角三角形的性质、三角形中位线定理的应用,掌握平行线的性质、三角形中位线定理、正确作出辅助性是解题的关键.

| A. | 平均数为2,众数为2,中位数为2 | B. | 平均数为3,众数为2,中位数为4 | ||
| C. | 平均数为2,众数为3,中位数为2 | D. | 平均数为2,众数为3,中位数为4 |

 已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.
已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.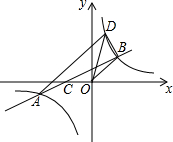 如图,点A和点B分别是反比例函数y=$\frac{k}{x}$(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=$\frac{1}{2}$,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D,连接OD,BD.
如图,点A和点B分别是反比例函数y=$\frac{k}{x}$(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=$\frac{1}{2}$,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D,连接OD,BD.