Question

13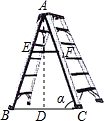．如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tanα=$\frac{5}{2}$，则“人字梯”的顶端离地面的高度AD是（　　）

• A． 144cm
• B． 180cm
• C． 240cm
• D． 360cm

Answer 1

分析 根据题意可知：△AEO∽△ABD，从而可求得BD的长，然后根据锐角三角函数的定义可求得AD的长．

解答 解：如图：

根据题意可知：△AFO∽△ACD，OF=$\frac{1}{2}$EF=30cm
∴$\frac{OF}{DC}=\frac{AF}{AC}$，
∴$\frac{30}{DC}=\frac{2.5}{6}$
∴CD=72cm，
∵tanα=$\frac{5}{2}$
∴$\frac{AD}{DC}=\frac{5}{2}$
∴AD=$\frac{5}{2}×72$=180cm．
故选：B．

点评 此题考查了三角函数的基本概念，主要是余弦概念及运算，关键把实际问题转化为数学问题加以计算．