题目内容
1. 如图,P是⊙O外一点,PO交⊙O于C点,PA和PB分别切⊙O于A和B点,已知⊙O的半径为3cm,∠APB=60°.若用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
如图,P是⊙O外一点,PO交⊙O于C点,PA和PB分别切⊙O于A和B点,已知⊙O的半径为3cm,∠APB=60°.若用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )| A. | 2$\sqrt{2}$cm | B. | $\sqrt{2}$cm | C. | $\sqrt{10}$cm | D. | $\frac{3}{2}$cm |
分析 首先根据扇形的圆心角和扇形的半径求得扇形的弧长,然后求得圆锥的底面半径,从而利用勾股定理求得圆锥的高.
解答 解:∵PA和PB分别切⊙O于A和B点,∠APB=60°,
∴∠AOB=120°,
∵半径为3cm,
∴扇形的弧长为$\frac{120π×3}{180}$=2π,
∴圆锥的底面半径为2π÷2π=1,
∴圆锥的高为$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$cm,
故选A.
点评 本题考查了切线的性质及圆锥的计算,解题的关键是能够求得扇形的圆心角的度数并求得扇形的弧长,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如果△ABC的∠A、∠B满足|2sinA-1|+(2cosB-$\sqrt{2}$)2=0,那么∠C的度数是( )
| A. | 45° | B. | 75° | C. | 90° | D. | 105° |
16. 如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
 如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
6.小颖本学期英语口语的检测成绩情况如表:
(1)请计算小颖本学期平时成绩的平均分;
(2)已知本学期英语口语总评成绩由平时成绩,期中成绩,期末成绩三部分组成,各部分比例分别为40%,20%,40%,总评成绩达到90分以上,可评定为A档,请问小颖要达到A档,期末成绩应不低于多少分?
| 测验 类别 | 平时成绩 | 期中 考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | ||
| 成绩 | 88 | 80 | 95 | 89 | 90 |
(2)已知本学期英语口语总评成绩由平时成绩,期中成绩,期末成绩三部分组成,各部分比例分别为40%,20%,40%,总评成绩达到90分以上,可评定为A档,请问小颖要达到A档,期末成绩应不低于多少分?
13.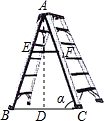 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )| A. | 144cm | B. | 180cm | C. | 240cm | D. | 360cm |
20. 从上面观察这个立体图形,能得到的平面图形是( )
从上面观察这个立体图形,能得到的平面图形是( )
 从上面观察这个立体图形,能得到的平面图形是( )
从上面观察这个立体图形,能得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,D是BC边上的一点,过A点作BC的平行线,截取AE=BD,连结EB,连结EC交AD于点F.
如图,在△ABC中,D是BC边上的一点,过A点作BC的平行线,截取AE=BD,连结EB,连结EC交AD于点F.