题目内容
5.如图,正方形ABCB1中,AB=1.AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2014A2015=2($\sqrt{3}$)2014.
分析 由四边形ABCB1是正方形,得到AB=AB1,AB∥CB1,于是得到AB∥A1C,根据平行线的性质得到∠CA1A=30°,解直角三角形得到A1B1=$\sqrt{3}$,AA1=2,同理:A2A3=22$\sqrt{3}$,A3A4=23$\sqrt{3}$,找出规律AnAn+1=2n$\sqrt{3}$,答案即可求出.
解答 解:∵四边形ABCB1是正方形,
∴AB=AB1,AB∥CB1,
∴AB∥A1C,
∴∠CA1A=30°,
∴A1B1=$\sqrt{3}$,AA1=2,
∴A1B2=A1B1=$\sqrt{3}$,
∴A1A2=2$\sqrt{3}$,
同理:A2A3=2($\sqrt{3}$)2,
A3A4=2($\sqrt{3}$)3,
…
∴AnAn+1=2($\sqrt{3}$)n,
∴A2014A2015=2($\sqrt{3}$)2014,
故答案为:2($\sqrt{3}$)2014.
点评 本题考查了正方形的性质,含30°直角三角形的性质,平行线的性质,熟记各性质并求出后一个正方形的边长是前一个正方形的边长的$\sqrt{3}$倍是解题的关键.

练习册系列答案
相关题目
16. 如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
 如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )
如图,A、C分别是x轴、y轴上的点,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
13.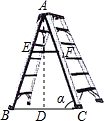 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )| A. | 144cm | B. | 180cm | C. | 240cm | D. | 360cm |
6.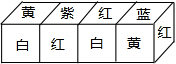 把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
将四个正方体拼成一个长方体如图位置,求此时长方体的下底的花朵数之和.
 把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
 如图,已知⊙O的半径为l,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点.
如图,已知⊙O的半径为l,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点.