题目内容
3.在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.则点M在直线y=x上的概率是$\frac{1}{3}$.分析 先画出数状图,展示所有9种等可能的结果数,再根据一次函数图象上点的坐标特征,找出在直线y=x上的点的个数,然后根据概率公式求解.
解答 解:画树状图为:
共有9种等可能的结果数,其中(1,1),(2,2),(3,3)在直线y=x上,
所以点M在直线y=x上的概率=$\frac{3}{9}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
14.为了解学生动地课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计,图(1)与图(2)是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( )


| A. | 由这两个统计图可知喜欢“科学常识”的学生有90人 | |
| B. | 若概年级共有12000名学生,则由这两个统计图可估计喜爱“科学常识”的学生有3600人 | |
| C. | 在扇形统计图汇总“漫画”所在扇形的圆心角为72° | |
| D. | 由这两个统计图不能确定喜欢”小说”的人数 |
18. 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于( )
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于( )
 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于( )
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
8.洛阳市某天的最高气温为l6℃,最低气温为-3℃,则这一天的最高气温与最低气温的差为( )
| A. | 13℃ | B. | 19℃ | C. | -13℃ | D. | -19℃ |
12.如果△ABC的∠A、∠B满足|2sinA-1|+(2cosB-$\sqrt{2}$)2=0,那么∠C的度数是( )
| A. | 45° | B. | 75° | C. | 90° | D. | 105° |
13.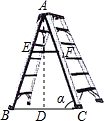 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )| A. | 144cm | B. | 180cm | C. | 240cm | D. | 360cm |
 如图,已知⊙O的半径为l,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点.
如图,已知⊙O的半径为l,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点.