题目内容
12.解方程:(1)(x+2)2=16.
(2)(1-x)2-18=0
(3)1-6x+9x2=1
(4)4x2+12x+9=25
(5)2($\sqrt{2}$x-3)2=12
(6)(3x-1)2=(3-2x)2.
分析 (1)方程利用平方根定义开方即可求出解;
(2)方程变形后,利用平方根定义开方即可求出解;
(3)方程变形后,利用配方法求出解即可;
(4)方程整理后,利用因式分解法求出解即可;
(5)方程变形后,利用直接开平方法求出解即可;
(6)方程利用两数的平方相等,两数相等或互为相反数,计算即可求出解.
解答 解:(1)开方得:x+2=4或x+2=-4,
解得:x1=2,x2=-6;
(2)方程变形得:(1-x)2=18,
开方得:1-x=±3$\sqrt{2}$,
解得:x1=1-3$\sqrt{2}$,x2=1+3$\sqrt{2}$;
(3)方程变形得:(3x-1)2=1,
开方得:3x-1=1或3x-1=-1,
解得:x1=$\frac{2}{3}$,x2=0;
(4)方程整理得:x2+3x-4=0,即(x-1)(x+4)=0,
解得:x1=1,x2=-4;
(5)方程变形得:($\sqrt{2}$x-3)2=6,
开方得:$\sqrt{2}$x-3=±$\sqrt{6}$,
解得:x1=$\frac{3\sqrt{2}+2\sqrt{3}}{2}$,x2=$\frac{3\sqrt{2}-2\sqrt{3}}{2}$;
(6)开方得:3x-1=3-2x或3x-1=2x-3,
解得:x1=$\frac{4}{5}$,x2=-2.
点评 此题考查了解一元二次方程-因式分解法,以及直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
13.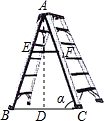 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是( )| A. | 144cm | B. | 180cm | C. | 240cm | D. | 360cm |
20. 从上面观察这个立体图形,能得到的平面图形是( )
从上面观察这个立体图形,能得到的平面图形是( )
 从上面观察这个立体图形,能得到的平面图形是( )
从上面观察这个立体图形,能得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
7.为了说明命题“当b<0时,关于x的一元二次方程x2+bx+2=0必有实数解”是假命题,可以举的一个反例是( )
| A. | b=2 | B. | b=3 | C. | b=-2 | D. | b=-3 |
1.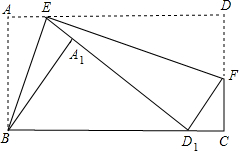 已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
 已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |