题目内容
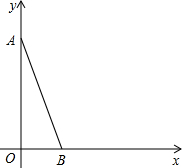 如图,在直角坐标系中,点A坐标为(0,5),点B的坐标为(2,0).
如图,在直角坐标系中,点A坐标为(0,5),点B的坐标为(2,0).(1)用直尺与圆规,求作一点C,满足CA=CB,并且CA∥OB;(不写作法,保留作图痕迹)
(2)求所作点C的坐标.
考点:作图—复杂作图,坐标与图形性质,勾股定理
专题:
分析:(1)作直线AC⊥y轴,与线段AB的垂直平分线交直线AC于点C,则点C即为所求点;
(2)连结CB,过点C作CD⊥x轴于点D,设AC=x,由题意得,OA=5,OB=2,OD=AC=x,则BD=x-2,再利用勾股定理可得,(x-2)2+52=x2,解方程可得x的值.
(2)连结CB,过点C作CD⊥x轴于点D,设AC=x,由题意得,OA=5,OB=2,OD=AC=x,则BD=x-2,再利用勾股定理可得,(x-2)2+52=x2,解方程可得x的值.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)连结CB,过点C作CD⊥x轴于点D,设AC=x,
由题意得,OA=5,OB=2,OD=AC=x,则BD=x-2,
由勾股定理得,(x-2)2+52=x2,
解之得,x=
,
所以点C的坐标为(
,5).
 解:(1)如图所示:
解:(1)如图所示:(2)连结CB,过点C作CD⊥x轴于点D,设AC=x,
由题意得,OA=5,OB=2,OD=AC=x,则BD=x-2,
由勾股定理得,(x-2)2+52=x2,
解之得,x=
| 29 |
| 4 |
所以点C的坐标为(
| 29 |
| 4 |
点评:此题主要考查了复杂作图,关键是正确画出图形,确定出C点位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
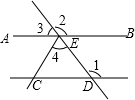 如图,EC平分∠AED,∠1=130°,若添加一个条件使得AB∥CD,下列不符合要求的是( )
如图,EC平分∠AED,∠1=130°,若添加一个条件使得AB∥CD,下列不符合要求的是( )| A、∠2=130° |
| B、∠4=75° |
| C、∠3=50° |
| D、∠2+∠4=195° |

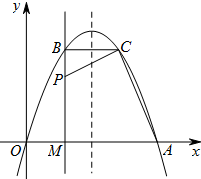 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.