题目内容
如图所示（图1为实景侧视图，图2为安装示意图），在屋顶的斜坡面上安装太阳能热水器：先安装支架AB和CD（均与水平面垂直），再将集热板安装在AD上．为使集热板吸热率更高，公司规定：AD与水平线夹角为θ1，且在水平线上的射影AF为140cm．现已测量出屋顶斜面与水平面夹角为θ2，并已知tanθ1≈1.1，tanθ2≈0.4．如果安装工人已确定支架AB高为25cm，求支架CD的高（结果精确到1cm）？
考点：解直角三角形的应用
专题：
分析：先根据矩形的性质得出AF=BE=140cm，AB=EF=25cm，再根据△DAF，△CBE是直角三角形可知，DF=AFtanθ1，CE=BEtanθ2，再由DE=DF+EF=，DC=DE-CE即可得出结论．
解答：解：∵矩形ABEF中，AF=BE=140cm，AB=EF=25cm．
Rt△DAF中，∠DAF=θ1，DF=AFtanθ1≈154cm，
Rt△CBE中，∠CBE=θ2，CE=BEtanθ2≈56cm，
∴DE=DF+EF=154+25=179cm，
DC=DE-CE=179-56=123cm．
答：支架CD的高为123cm．
Rt△DAF中，∠DAF=θ1，DF=AFtanθ1≈154cm，
Rt△CBE中，∠CBE=θ2，CE=BEtanθ2≈56cm，
∴DE=DF+EF=154+25=179cm，
DC=DE-CE=179-56=123cm．
答：支架CD的高为123cm．
点评：本题考查的是解直角三角形的应用，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，∠A=120°，AB的垂直平分线交BC于点D，交AB于点B，如果DE=1，求BC的长．
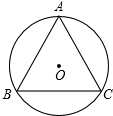如图，等边三角形ABC的三个顶点都在圆上．这个图形是中心对称图形吗？如果是，指出它的对称中心，并画出该图关于点A对称的图形；如果不是，请在圆内补上一个三角形，使整个图形成为中心对称图形（保留画图痕迹），并指出所补三角形可以看作由△ABC怎样变换而成的．
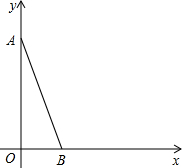如图，在直角坐标系中，点A坐标为（0，5），点B的坐标为（2，0）．
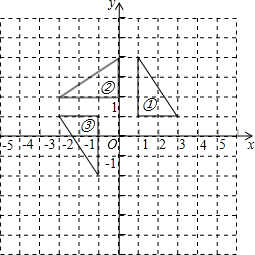如图，在平面直角坐标系中，三角形②、③是由三角形①依次绕点P旋转后所得的图形．
如图，在平行四边形ABCD中，BD=CD，∠A=75°，CE⊥BD于E，求∠BCE的度数．