题目内容
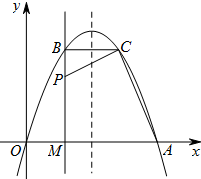 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.(1)当m=
| 5 |
| 2 |
(2)当m>1时,连接CA,当CA⊥CP时,求m的值;
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E恰好落在坐标轴上?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把m=
,代入抛物线的解析式,令y=0解方程,得到的非0解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;
(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△ACH∽△PCB,根据相似的性质得到:
=
,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;
(3)存在,本题要分当m>1时,BC=2(m-1),PM=m,BP=m-1和当0<m<1时,BC=2(1-m),PM=m,BP=1-m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.
| 5 |
| 2 |
(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△ACH∽△PCB,根据相似的性质得到:
| AH |
| CH |
| PB |
| BC |
(3)存在,本题要分当m>1时,BC=2(m-1),PM=m,BP=m-1和当0<m<1时,BC=2(1-m),PM=m,BP=1-m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.
解答: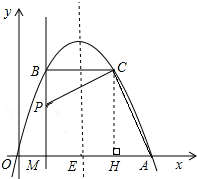 解:(1)当m=
解:(1)当m=
时,y=-x2+5x;
令y=0,得-x2+5x=0.
∴x1=0,x2=5,
∴A(5,0).
当x=1时,y=4,
∴B(1,4).
∵抛物线y=-x2+5x的对称轴为直线x=
,
又∵点B,C关于对称轴对称,
∴BC=3;
(2)过点C作CH⊥x轴于点H(如图).
由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB.
又∵∠AHC=∠PBC=90°,
tan∠ACH=tan∠PCB.
∴
=
.
∵抛物线y=-x2+2mx的对称轴为直线x=m,其中m>1,
又∵B,C关于对称轴对称,
∴BC=2(m-1).
∵B(1,2m-1),P(1,m),
∴BP=m-1.
又∵A(2m,0),C(2m-1,2m-1),
∴H(2m-1,0).
∴AH=1,CH=2m-1.
∴
=
,
∴m=
;
(3)存在.
∵B,C不重合,
∴m≠1,分两种情况:
①当m>1时,m=2,相对应的E点坐标是(2,0)或(0,4);
②当0<m<1时,m=
.,相对应的E点坐标是(
,0);
∴E点坐标是(2,0)或(0,4)或(
,0).
 解:(1)当m=
解:(1)当m=| 5 |
| 2 |
令y=0,得-x2+5x=0.
∴x1=0,x2=5,
∴A(5,0).
当x=1时,y=4,
∴B(1,4).
∵抛物线y=-x2+5x的对称轴为直线x=
| 5 |
| 2 |
又∵点B,C关于对称轴对称,
∴BC=3;
(2)过点C作CH⊥x轴于点H(如图).
由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB.
又∵∠AHC=∠PBC=90°,
tan∠ACH=tan∠PCB.
∴
| AH |
| CH |
| PB |
| BC |
∵抛物线y=-x2+2mx的对称轴为直线x=m,其中m>1,
又∵B,C关于对称轴对称,
∴BC=2(m-1).
∵B(1,2m-1),P(1,m),
∴BP=m-1.
又∵A(2m,0),C(2m-1,2m-1),
∴H(2m-1,0).
∴AH=1,CH=2m-1.
∴
| 1 |
| 2m-1 |
| m-1 |
| 2(m-1) |
∴m=
| 3 |
| 2 |
(3)存在.
∵B,C不重合,
∴m≠1,分两种情况:
①当m>1时,m=2,相对应的E点坐标是(2,0)或(0,4);
②当0<m<1时,m=
| 2 |
| 3 |
| 4 |
| 3 |
∴E点坐标是(2,0)或(0,4)或(
| 4 |
| 3 |
点评:此题主要考查了二次函数解析式的确定、轴对称的性质、相似三角形的判定和相似三角形的性质以及全等三角形的性质和全等三角形的判定、需注意的是(3)题在不确E点的情况下需要分类讨论,以免漏解.题目的综合性强,难度也很大,有利于提高学生的综合解题能力,是一道不错的题目.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列计算正确的是( )
| A、(a3)4=a7 |
| B、a8÷a4=a2 |
| C、(2a2)3•a3=8a9 |
| D、4a5-2a5=2 |
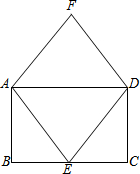 如图,四边形ABCD为矩形,四边形AEDF为菱形.
如图,四边形ABCD为矩形,四边形AEDF为菱形.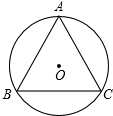 如图,等边三角形ABC的三个顶点都在圆上.这个图形是中心对称图形吗?如果是,指出它的对称中心,并画出该图关于点A对称的图形;如果不是,请在圆内补上一个三角形,使整个图形成为中心对称图形(保留画图痕迹),并指出所补三角形可以看作由△ABC怎样变换而成的.
如图,等边三角形ABC的三个顶点都在圆上.这个图形是中心对称图形吗?如果是,指出它的对称中心,并画出该图关于点A对称的图形;如果不是,请在圆内补上一个三角形,使整个图形成为中心对称图形(保留画图痕迹),并指出所补三角形可以看作由△ABC怎样变换而成的. 如图,以O为圆心的弧
如图,以O为圆心的弧
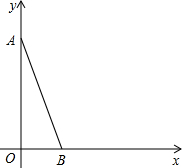 如图,在直角坐标系中,点A坐标为(0,5),点B的坐标为(2,0).
如图,在直角坐标系中,点A坐标为(0,5),点B的坐标为(2,0).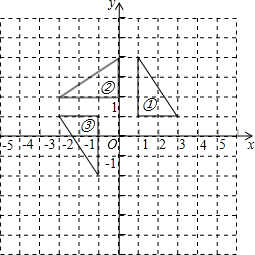 如图,在平面直角坐标系中,三角形②、③是由三角形①依次绕点P旋转后所得的图形.
如图,在平面直角坐标系中,三角形②、③是由三角形①依次绕点P旋转后所得的图形.