题目内容
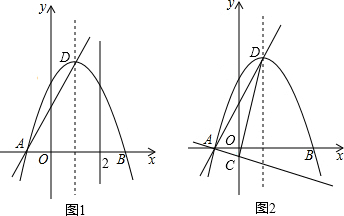
2.若一个圆经过正方形的对称中心,则称此圆为该正方形的“伴侣圆:”,如图1,正方形ABCD的边长为a,对角线交于点E,已知⊙O是正方形ABCD的“伴侣圆”,其半径为r.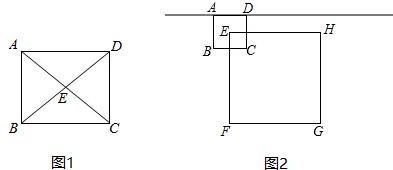
(1)当r=1,a=2时,圆心O可以是C.
A.点A B.点E C.线段AB的中点 D.线段AE的中点
(2)如果圆心O在正方形ABCD的边上,且a=1,那么r的取值范围为$\frac{1}{2}$≤r$≤\frac{\sqrt{2}}{2}$.
(3)如果r=1,⊙O与正方形ABCD的四边最多有2个公共点,那么a的取值范围为0<a≤2或a≥2+$\sqrt{2}$.
(4)如果⊙O同时也是边长为3的正方形EFGH的“伴侣圆”,且EF∥AB,a=1,如图2,求当⊙O与直线AB相切时r的值.
分析 (1)根据伴侣圆的定义,圆O经过正方形ABCD对角线的交点E,圆心到点E距离为1,分析得C符合要求;
(2)当圆心O在正方形ABCD四条边的中点时,其半径r最小,当圆心O在正方形ABCD的四个顶点时,半径最大,分别求出半径的最大值,最小值即可.
(3)从大到小画出6种图形即可解决问题.
(4)连接EG,FH交于点O,设⊙O和AB相切于点M,设半径为r,作OK⊥EG于K,交AB于J,由题意AE=EC=$\frac{\sqrt{2}}{2}$,EN=$\frac{3}{2}$$\sqrt{2}$,推出EK=KN=$\frac{3}{4}$$\sqrt{2}$,AK=KJ=$\frac{5\sqrt{2}}{4}$,在Rt△OKN中,根据OK2+KN2=ON2,列出方程即可解决问题.
解答 解:(1)由正方形性质得,
点A至点E距离为:$\frac{1}{2}$AC=$\frac{1}{2}$$\sqrt{{2}^{2}{+2}^{2}}$=$\sqrt{2}$,
点E至点E距离为:0,
线段AB的中点至点E距离为1,
线段AE的中点至点E距离为:$\frac{\sqrt{2}}{2}$,
故选C.
(2)当圆心O在正方形ABCD四条边的中点时,其半径r最小为$\frac{1}{2}a$=$\frac{1}{2}×1$=$\frac{1}{2}$,
当圆心O在正方形ABCD的四个顶点时,其半径r最大为$\frac{1}{2}$×$\sqrt{{1}^{2}{+1}^{2}}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{1}{2}$≤r$≤\frac{\sqrt{2}}{2}$;
故答案为:$\frac{1}{2}$≤r$≤\frac{\sqrt{2}}{2}$;
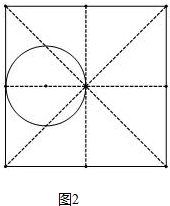
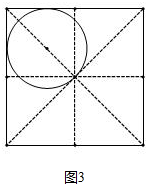
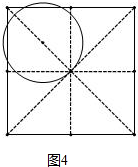
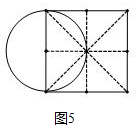
(3)如图①~⑥正方形的边长不断缩小,①②③三种情形圆与正方形最多有2个公共点,图③时,a=2+$\sqrt{2}$,图④时交点超过2个,图⑤⑥两种情形是两个交点,
图⑤时,a=2,综上所述0<a≤2或a≥2+$\sqrt{2}$.
故答案为0<a≤2或a≥2+$\sqrt{2}$.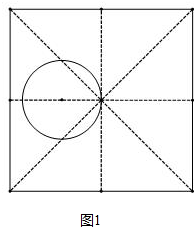
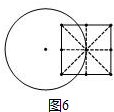
(4)连接EG,FH交于点O,设⊙O和AB相切于点M,设半径为r,
作OK⊥EG于K,交AB于J,由题意AE=EC=$\frac{\sqrt{2}}{2}$,EN=$\frac{3}{2}$$\sqrt{2}$,
∴EK=KN=$\frac{3}{4}$$\sqrt{2}$,AK=KJ=$\frac{5\sqrt{2}}{4}$,
在Rt△OKN中,∵OK2+KN2=ON2,
∴($\frac{5\sqrt{2}}{4}$-$\sqrt{2}$r)2+($\frac{3}{4}$$\sqrt{2}$)2=r2,
解得r=$\frac{5±2\sqrt{2}}{2}$,
∴当⊙O与直线AB相切时r的值为$\frac{5±2\sqrt{2}}{2}$.
点评 本题考查圆的有关性质、正方形的性质、勾股定理等知识,综合性比较强,解题的关键是正确画出图形,学会转化为方程的思想解决问题,熟练掌握特殊三角形边之间的关系,属于中考压轴题.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | a3+a3=a6 | B. | a3•a2=a6 | C. | (-a3)2=a9 | D. | (-a2)3=-a6 |
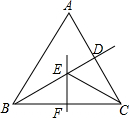 如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )| A. | 24° | B. | 30° | C. | 32° | D. | 36° |