题目内容
12．已知a＜b＜c，x＜y＜z．则下列四个式子：甲：ax+by+cz；乙：ax+bz+cy；丙：ay+bx+cz；丁：az+bx+cy中，值最大的一个必定是（ ）| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
分析 要比较两个多项式的大小，只需采用作差法，将它们的差因式分解就可解决问题．
解答 解：∵b＜c，y＜z，
∴b-c＜0，y-z＜0，
∴（ax+by+cz）-（ax+bz+cy）=by+cz-bz-cy=b（y-z）-c（y-z）=（y-z）（b-c）＞0，
∴ax+by+cz＞ax+bz+cy．
同理：ax+by+cz＞ay+bx+cz，ax+bz+cy＞az+bx+cy，
∴ax+by+cz＞ax+bz+cy＞az+bx+cy，
∴甲最大．
故选A．
点评 本题主要考查了整式的加减、因式分解、不等式的性质、不等式的传递性等知识，比较大小常用作差法或作商法，应熟练掌握．
练习册系列答案
相关题目
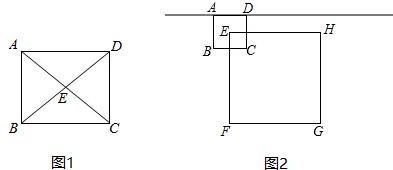
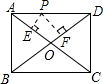如图，P是矩形的边AD上一个动点，AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是2.4．
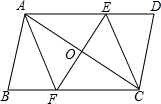已知：如图，在?ABCD中，线段EF分别交AD、AC、BC于点E、O、F，EF⊥AC，AO=CO．
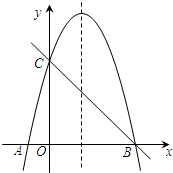如图，抛物线y=ax2+bx-4a的对称轴为直线x=$\frac{3}{2}$，与x轴交于A，B两点，与y轴交于点C（0，4）．