题目内容
如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
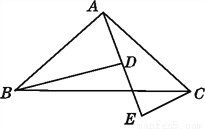
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
（1）见解析；（2）∠ADB=90°
【解析】试题分析：（1）根据全等三角形的性质求出BD=AE，AD=CE，代入求出即可；
（2）根据全等三角形的性质求出∠E=∠BDA=90°，推出∠BDE=90°，根据平行线的判定求出即可．
试题解析: (1)∵△BAD≌△ACE，
∴BD=AE，AD=CE，
∴BD=AE=AD+DE=CE+DE，
即BD=DE+CE；
...
练习册系列答案
相关题目
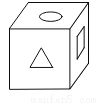
下面四个图形中，经过折叠能围成如图1，只有三个面上印有图案的正方体纸盒的是（ ）
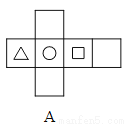
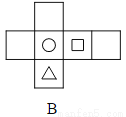
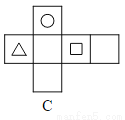
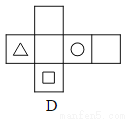
B
【解析】本题考查的是正方体的展开图
根据图中符号所处的位置关系作答．
三角形图案的顶点应与圆形的图案相对，而选项A，C与此不符，所以错误；
三角形图案所在的面应与圆形的图案所在的面相邻，而选项D与此也不符，正确的是B，
故选B． 如图，已知线段AB的垂直平分线CP交AB于点P，且AP=2PC，现欲在线段AB上求作两点D，E，使其满足AD=DC=CE=EB，对于以下甲、乙两种作法：
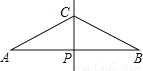
甲：分别作∠ACP、∠BCP的平分线，分别交AB于D、E，则D、E即为所求；乙：分别作AC、BC的垂直平分线，分别交AB于D、E，则D、E两点即为所求．下列说法正确的是（ ）
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确，乙错误 D. 甲错误，乙正确
D
【解析】试题解析：甲：虽然CP=AP，
但∠A≠∠ACP，
即∠A≠∠ACD．甲不正确；
乙∵CP是线段AB的中垂线，
∴△ABC是等腰三角形，即AC=BC，∠A=∠B，
作AC、BC之中垂线分别交AB于D、E，
∴∠A=∠ACD，∠B=∠BCE，
∵∠A=∠B，
∴∠A=∠ACD，∠B=∠BCE，
∵AC=BC，
∴△ACD≌... 如图，将两根钢条AA′，BB′ 的中点O钉在一起，使AA′，BB′ 能绕点O自由转动，就做成一个测量工具，测A′B′ 的长即等于内槽宽AB，那么判定△OAB ≌△OA′B′的理由是（ ）．
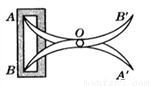
A. 边角边 B. 角边角 C. 边边边 D. 斜边直角边
A
【解析】由题意得边角边可得全等.故选A. 如图，AB∥CD，AD∥BC；则图中的全等三角形共有（ ）
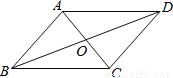
A. 5对 B. 4对 C. 3对 D. 2对
B
【解析】∵AB∥CD，AD∥BC，
∴四边形ABCD为平行四边形，
∴AB=CD，AD=BC，AO=CO，BO=DO，EO=FO，∠DAO=∠BCO，
又∠AOB=∠COD，∠AOD=∠COB，∠AOE=∠COF，
∴△AOB≌△COD（SSS），△AOD≌△COB（SSS），△ABC≌△CDA（SSS），△ABD≌△CDB（SSS）.
故图中的全等三角形共... 如图,已知△ABD≌△CDB,∠ABD=∠CDB,写出其余的对应边和对应角.
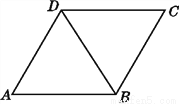
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析：∵△ABD≌△CDB，
∴∴AB的对应边是CD，AD的对应边是CB，BD的对应边是DB，
∠A的对应角是∠C，∠ADB的对应角是∠CBD，∠ACB的对应角是∠ECD. 若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A. BC=EF B. ∠B=∠D
C. ∠C=∠F D. AC=EF
A
【解析】∵点A和点E，点B和点D分别是对应点，
∴△ABC≌△EDF，
∴∠A=∠E，∠B=∠D，∠C=∠F，AC=EF，BC=DF，AB=ED.
故选：A. 如图，直线l1∥l2，若∠1=130°，∠2=60°，则∠3= ．
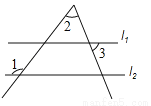
70°．
【解析】
试题分析：∵直线l1∥l2，∴∠4=∠1=130°，∴∠5=∠4﹣∠2=70°，∴∠5=∠3=70°．，故答案为：70°． 已知a是－2的相反数，且|b＋1|＝0，则[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)的值为_____.
5
【解析】[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)
=
=
=
∵a是－2的相反数，且|b＋1|＝0，
∴a=2，b=-1，
∴原式==-1+6=5.