题目内容
(2x-y)2·(2x+y)2
 16x4-8x2y2+y4
【解析】试题分析:根据积的乘方的运算法则把(2x-y)2·(2x+y)2转化为后,先利用平方差公式计算,再利用完全平方公式计算即可.
试题解析:
(2x-y)2·(2x+y)2
=
=
=16x4-8x2y2+y4
16x4-8x2y2+y4
【解析】试题分析:根据积的乘方的运算法则把(2x-y)2·(2x+y)2转化为后,先利用平方差公式计算,再利用完全平方公式计算即可.
试题解析:
(2x-y)2·(2x+y)2
=
=
=16x4-8x2y2+y4
练习册系列答案
相关题目
如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
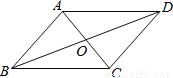
A. 5对 B. 4对 C. 3对 D. 2对
 B
【解析】∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共...
B
【解析】∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共... 在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
A. 4cm B. 5cm C. 9cm D. 13cm
 C
【解析】试题解析:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,
即9-4=5,9+4=13.
∴第三边取值范围应该为:5<第三边长度<13,
故只有C选项符合条件.
故选C.
C
【解析】试题解析:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,
即9-4=5,9+4=13.
∴第三边取值范围应该为:5<第三边长度<13,
故只有C选项符合条件.
故选C. 如果x2+ax+9=(x+3)2,那么a的值为( )
A. 3 B. ±3 C. 6 D. ±6
 C
【解析】∵x2+ax+9=(x+3)2,而(x+3)2=x2+6x+9;即x2+ax+9=x2
C
【解析】∵x2+ax+9=(x+3)2,而(x+3)2=x2+6x+9;即x2+ax+9=x2 下列运算正确的是( )
A. 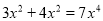 B.
B. 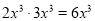 C.
C. 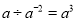 D.
D. 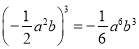
 C
【解析】根据合并同类项法则,可知,故不正确;
根据单项式乘以单项式和同底数幂相乘,可知,故不正确;
根据同底数幂相除,可知,故正确;
根据积的乘方,可知,故不正确.
故选:C.
C
【解析】根据合并同类项法则,可知,故不正确;
根据单项式乘以单项式和同底数幂相乘,可知,故不正确;
根据同底数幂相除,可知,故正确;
根据积的乘方,可知,故不正确.
故选:C. 已知a是-2的相反数,且|b+1|=0,则[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)的值为_____.
 5
【解析】[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)
=
=
=
∵a是-2的相反数,且|b+1|=0,
∴a=2,b=-1,
∴原式==-1+6=5.
5
【解析】[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)
=
=
=
∵a是-2的相反数,且|b+1|=0,
∴a=2,b=-1,
∴原式==-1+6=5. 已知(x-2 015)2+(x-2 017)2=34,则(x-2 016)2的值是( )
A. 4 B. 8 C. 12 D. 16
 D
【解析】(x-2 015)2+(x-2 017)2
=(x-2 016+1)2+(x-2 016-1)2
=
==34
∴
故选D.
D
【解析】(x-2 015)2+(x-2 017)2
=(x-2 016+1)2+(x-2 016-1)2
=
==34
∴
故选D. 如图,两个边长分别为4cm与3cm的正方形的一部分重叠在一起,重叠部分是边长为acm的正方形,则图中阴影部分的面积总和是_____cm2.面积之差是_____cm2

 , 7
【解析】试题分析:阴影部分的面积总和是:42-a2+32-a2=25-2a2(cm2);
阴影部分面积之差是:(42-a2)-(32-a2)=7(cm2).
故答案为:25-2a2;7.
, 7
【解析】试题分析:阴影部分的面积总和是:42-a2+32-a2=25-2a2(cm2);
阴影部分面积之差是:(42-a2)-(32-a2)=7(cm2).
故答案为:25-2a2;7. 一个不透明的口袋内装有50个大小材质相同且编号不同的小球,它们按照从1到50依次编号,将袋中的小球搅匀,然后从中随意取出一个小球,请问
(1)取出的小球编号是偶数的概率是多少?
(2)取出的小球编号是3的倍数的概率是多少?
(3)取出的小球编号是质数的概率是多少?
 (1) (2) (3)
【解析】分析:本题考察对概率意义的理解,关键是找出各种符合条件的编号的个数.
本题解析:
(1)一个不透明的口袋内装有50个大小材质相同且编号不同的小球,它们按照从1到50依次编号,将袋中的小球搅匀,然后从中随意取出一个小球,那么每一个小球被取到的概率是相同的.这其中,编号为偶数的有25个,所以取出的小球编号是偶数的概率是.
(2)一个不透明的口袋内...
(1) (2) (3)
【解析】分析:本题考察对概率意义的理解,关键是找出各种符合条件的编号的个数.
本题解析:
(1)一个不透明的口袋内装有50个大小材质相同且编号不同的小球,它们按照从1到50依次编号,将袋中的小球搅匀,然后从中随意取出一个小球,那么每一个小球被取到的概率是相同的.这其中,编号为偶数的有25个,所以取出的小球编号是偶数的概率是.
(2)一个不透明的口袋内... 
