题目内容
10.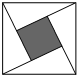 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.学习《探索勾股定理》后,几位同学在上课用的道具上玩掷骰子的游戏,看谁能把骰子投到中间的小正方形中.若设直角三角形的两条直角边的长分别是1和2.你能算出骰子投在在中间小正方形区域(含边线)的概率吗?是$\frac{1}{5}$.
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.学习《探索勾股定理》后,几位同学在上课用的道具上玩掷骰子的游戏,看谁能把骰子投到中间的小正方形中.若设直角三角形的两条直角边的长分别是1和2.你能算出骰子投在在中间小正方形区域(含边线)的概率吗?是$\frac{1}{5}$.
分析 设大正方形的边长是a,则有:22+12=a2,则a2=5,即正方形ABCD的面积为5;阴影部分(小正方形)边长为2-1=1,面积为1;求骰子投在在中间小正方形区域的概率,即求1是5的几分之几,用除法解答即可.
解答 解:设大正方形的边长是a,则有:22+12=a2,则a2=5;阴影部分(小正方形)边长为2-1=1,面积为1,
则骰子投在在中间小正方形区域的概率P=1÷5=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 此题考查几何概率的求法,求得阴影部分小正方形的面积和大正方形面积,进而用两个正方形面积比得出结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC为等边三角形,点P(x,y)在△ABC内随机移动,求x>y的概率.
如图,△ABC为等边三角形,点P(x,y)在△ABC内随机移动,求x>y的概率.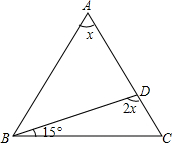 如图,在△ABC中,∠ABC=∠ACB,求∠ADB度数.
如图,在△ABC中,∠ABC=∠ACB,求∠ADB度数.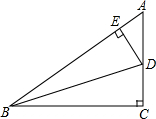 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6,求△AED的周长.
在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6,求△AED的周长.