题目内容
1．观察下面的几个算式：1+2+1=4=2×2；
1+2+3+2+1=9=3×3；
1+2+3+4+3+2=16=4×4；
1+2+3+4+5+4+3+2+1=25=5×5．
根据上面几道题的规律，计算下面的题：
（1）1+2+3+…+9+…+3+2+1；
（2）1+2+3+…+n+…+3+2+1．
分析 由题意可知：从1开始连续加到几，再逆着顺序加到1，计算结果是中间数字的平方．根据规律解题即可．
解答 解：（1）1+2+3+…+9+…+3+2+1=92=81；
（2）1+2+3+…+n+…+3+2+1=n2．
点评 此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题．
练习册系列答案
相关题目
9．2011年世界园艺博览会在西安隆重开园，这次世园会的个人票设置有三种：
某社区居委会为奖励“和谐家庭”，欲购买个人票100张，其中B种票张数是A种票张数的3倍还多8张．设需购A种票张数为x，C种票张数为y．
（1）写出y与x之间的函数关系式；
（2）设购票总费用为w元，求出w（元）与x（张）之间的函数关系式．
| 票的种类 | 夜票（A） | 平日普通票（B） | 指定日普通票（C） |
| 单价（元/张） | 60 | 100 | 150 |
（1）写出y与x之间的函数关系式；
（2）设购票总费用为w元，求出w（元）与x（张）之间的函数关系式．
16．若分式$\frac{{x}^{2}-7x-8}{x+1}$的值为0，则x的值为（ ）
| A． | -1 | B． | 8 | C． | -1或8 | D． | -8 |
13．下列各式中正确的是（ ）
| A． | $\sqrt{4}$=±2 | B． | $\sqrt{{3^2}+{4^2}}$=7 | C． | $\sqrt{（-\frac{1}{2}}{）^2}=-\frac{1}{2}$ | D． | $\sqrt{2\frac{1}{4}}=1\frac{1}{2}$ |
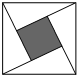“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．学习《探索勾股定理》后，几位同学在上课用的道具上玩掷骰子的游戏，看谁能把骰子投到中间的小正方形中．若设直角三角形的两条直角边的长分别是1和2．你能算出骰子投在在中间小正方形区域（含边线）的概率吗？是$\frac{1}{5}$．
