题目内容
20．
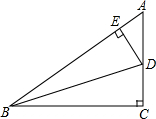在Rt△ABC中，BD平分∠ABC，DE⊥AB于E，若AB=10，BC=8，AC=6，求△AED的周长．
分析 根据角平分线的性质得到DE=DC，证明Rt△BED≌Rt△BCD，得到BE=BC=8，求出AE的长，根据三角形的周长公式计算即可．
解答 解：∵BD平分∠ABC，DE⊥AB，∠C=90°，
∴DE=DC，
在Rt△BED和Rt△BCD中，
$\left\{\begin{array}{l}{DE=DC}\\{BD=BD}\end{array}\right.$，
∴Rt△BED≌Rt△BCD，
∴BE=BC=8，
∴AE=AB-BE=2，
则△AED的周长=AE+ED+AD=AE+DC+AD=2+6=8．
点评 本题考查的是角平分线的性质和全等三角形的判定，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
相关题目
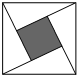“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．学习《探索勾股定理》后，几位同学在上课用的道具上玩掷骰子的游戏，看谁能把骰子投到中间的小正方形中．若设直角三角形的两条直角边的长分别是1和2．你能算出骰子投在在中间小正方形区域（含边线）的概率吗？是$\frac{1}{5}$．
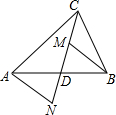如图，CD为△ABC的中线，M、N分别为直线CD上的点，且BM∥AN．
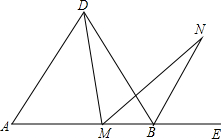已知点M是等边△ABD中边AB上任意一点（不与A、B重合），作∠DMN=60°，交∠DBA外角平分线于点N．