题目内容
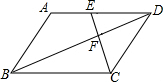如图，在平行四边形ABCD中，点E是边AD上的一点，且AE：ED=2：3，EC交对角线BD于点F，则EF：FC等于（ ）| A、3：2 | B、2：5 |
| C、2：3 | D、3：5 |
考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：如图，证明△DEF∽△CBF，得到
=
；设AE=2λ，得到DE=3λ，BC=5λ；得到
=
，即可解决问题．
| EF |
| FC |
| DE |
| BC |
| EF |
| FC |
| 3λ |
| 5λ |
解答：解：如图，∵四边形ABCD为平行四边形，
∴ED∥BC，BC=AD；
∴△DEF∽△CBF，
=
；
设AE=2λ，则DE=3λ，BC=5λ；
∴
=
，故选D．
解：如图，∵四边形ABCD为平行四边形，∴ED∥BC，BC=AD；
∴△DEF∽△CBF，
| EF |
| FC |
| DE |
| BC |
设AE=2λ，则DE=3λ，BC=5λ；
∴
| EF |
| FC |
| 3λ |
| 5λ |
点评：该题主要考查了平行四边形的性质、相似三角形判定及其性质等几何知识点及其应用问题；应牢固掌握平行四边形的性质、相似三角形判定及其性质．
练习册系列答案
相关题目
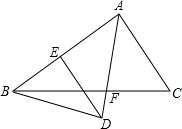如图，AF是△ABC的角平分线，BD⊥AF交AF的延长线于D，DE∥AC，交AB于E，AE与BE相等吗？请说明理由．
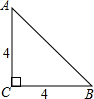已知如图，是腰长为4的等腰直角三角形ABC，要求在其内部作出一个半圆，直径在△ABC的边上，且半圆的弧与△ABC的其他两边相切，则该半圆的半径是
如图，在△ABC中，
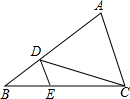如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若S△DEC：S△ADC=1：3，则S△BDE：S△ACD=
已知等腰三角形的两边长分别为6和5，则这个等腰三角形的周长是（ ）
| A、15或16 | B、16 |
| C、17 | D、16或17 |
