题目内容
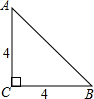 已知如图,是腰长为4的等腰直角三角形ABC,要求在其内部作出一个半圆,直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则该半圆的半径是
已知如图,是腰长为4的等腰直角三角形ABC,要求在其内部作出一个半圆,直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则该半圆的半径是考点:直线与圆的位置关系
专题:分类讨论
分析:分两种情况:①是直径在斜边上;②是直径在腰上分别求解半圆半径的长即可.
解答:解:①∵半圆的直径在△ABC的斜边上,且半圆的弧与△ABC的两腰相切,切点为D、E,
如图1,连接OD,OA,
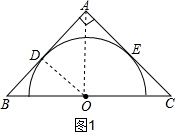
∵AB与⊙O相切,
∴OD⊥AB,
∵在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,
∴AO⊥BC,
∴OD∥AC,
∵O为BC的中点,
∴OD=
AC=2.
②∵半圆的直径在△ABC的腰上,且半圆的弧与△ABC的斜边相切,切点为D,
如图2,连接OD,设半圆的半径为r,
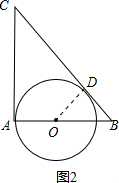
∴OB=4-r,
∵在等腰直角三角形ABC中,AB=AC=4,
∴∠B=45°,
∴△OBD是等腰直角三角形,
∴OD=BD=r,
∴2r2=(4-r)2,解得r=-4+4
,r=-4-4
(舍去),
故答案为:2或-4+4
.
如图1,连接OD,OA,

∵AB与⊙O相切,
∴OD⊥AB,
∵在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,
∴AO⊥BC,
∴OD∥AC,
∵O为BC的中点,
∴OD=
| 1 |
| 2 |
②∵半圆的直径在△ABC的腰上,且半圆的弧与△ABC的斜边相切,切点为D,
如图2,连接OD,设半圆的半径为r,

∴OB=4-r,
∵在等腰直角三角形ABC中,AB=AC=4,
∴∠B=45°,
∴△OBD是等腰直角三角形,
∴OD=BD=r,
∴2r2=(4-r)2,解得r=-4+4
| 2 |
| 2 |
故答案为:2或-4+4
| 2 |
点评:本题主要考查了切线的性质、切线长定理以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
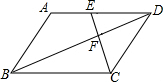 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
甲、乙两人都去同一家超市购买大米各两次,甲每次购买50千克的大米,乙每次够买50元的大米,这两人第一次够买大米时售价为每千克m元,第二次够买大米时售价为每千克n元(m≠n),若规定谁两次够买大米的平均单价低,谁的够买方式就合算,则( )
| A、甲的够买方式合算 |
| B、乙的够买方式合算 |
| C、甲、乙的够买方式同样合算 |
| D、不能判断谁的够买方式合算 |
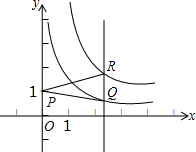 函数y=
函数y= 如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=
如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=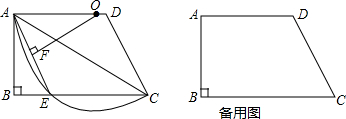
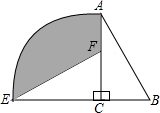 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=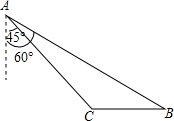 如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:
如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据: