题目内容
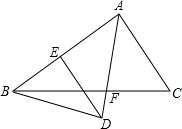 如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC,交AB于E,AE与BE相等吗?请说明理由.
如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC,交AB于E,AE与BE相等吗?请说明理由.考点:全等三角形的判定与性质,角平分线的性质
专题:计算题
分析:AE=BE,理由为:由AF为角平分线,得到一对角相等,再由DE与AC平行,得到一对内错角相等,等量代换得到∠EAD=∠ADE,利用等角对等边得到AE=DE,由BD与AF垂直得到一对角互余,利用等角的余角相等得到∠EBD=∠EDB,利用等角对等边得到BE=DE,等量代换即可得证.
解答:解:AE=BE,理由为:
∵AF平分∠BAC,
∴∠EAD=∠CAD,
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠EAD=∠ADE,
∴AE=DE,
∵BD⊥AF,
∴∠EDB+∠ADE=90°,
∵∠BDE+∠BAD=90°,
∴∠EBD+∠BAD=90°,
∴∠BDE=∠EBD,
∴BE=ED,
∴AE=BE.
∵AF平分∠BAC,
∴∠EAD=∠CAD,
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠EAD=∠ADE,
∴AE=DE,
∵BD⊥AF,
∴∠EDB+∠ADE=90°,
∵∠BDE+∠BAD=90°,
∴∠EBD+∠BAD=90°,
∴∠BDE=∠EBD,
∴BE=ED,
∴AE=BE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
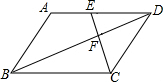 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
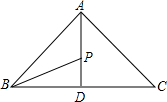 如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.
如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.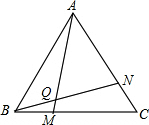 △ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点.
△ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点.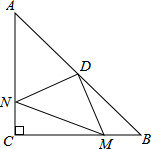 在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.
在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.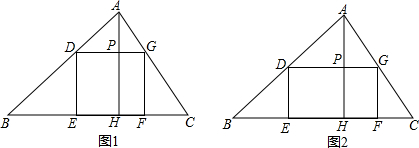
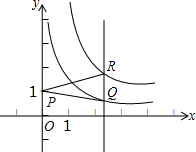 函数y=
函数y= 如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=
如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=