题目内容
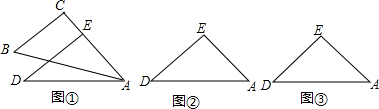
一幅直角三角形叠放如图①所示,其中直角边AC与AE重合,斜边AB与AD在AC的同侧,现将含45°角的三角板ADE固定不动,含30°角的三角板ABC绕顶点A顺时针旋转角a(0°<a<180°),使两块三角板至少有一组边平行.
(1)求图①中∠BAD的度数;
(2)请你在图②,③中各画一种符合要求的图形,并写出对应的a的度数和平行线段.
(1)求图①中∠BAD的度数;
(2)请你在图②,③中各画一种符合要求的图形,并写出对应的a的度数和平行线段.

考点:平行线的性质
专题:
分析:(1)根据∠BAD=∠DAE-∠BAC计算即可得解;
(2)根据图形作出BC∥AD和AC∥DE两种情况的图形,然后根据平行线的性质写出旋转角即可.
(2)根据图形作出BC∥AD和AC∥DE两种情况的图形,然后根据平行线的性质写出旋转角即可.
解答: 解:(1)∠BAD=∠DAE-∠BAC
解:(1)∠BAD=∠DAE-∠BAC
=45°-30°
=15°;
(2)如图②若BC∥AD,则α=90°-30°=60°,
如图③,若AC∥DE,则α=∠CAD-∠BAC=(180°-45°)-30°=105°.
 解:(1)∠BAD=∠DAE-∠BAC
解:(1)∠BAD=∠DAE-∠BAC=45°-30°
=15°;
(2)如图②若BC∥AD,则α=90°-30°=60°,
如图③,若AC∥DE,则α=∠CAD-∠BAC=(180°-45°)-30°=105°.
点评:本题考查了平行线的性质,旋转,三角尺的知识,熟记性质是解题的关键,难点在于(2)根据对应边的不同作出图形.

练习册系列答案
相关题目
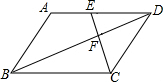 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
甲、乙两人都去同一家超市购买大米各两次,甲每次购买50千克的大米,乙每次够买50元的大米,这两人第一次够买大米时售价为每千克m元,第二次够买大米时售价为每千克n元(m≠n),若规定谁两次够买大米的平均单价低,谁的够买方式就合算,则( )
| A、甲的够买方式合算 |
| B、乙的够买方式合算 |
| C、甲、乙的够买方式同样合算 |
| D、不能判断谁的够买方式合算 |
要由抛物线y=5x2得到抛物线y=5(x-1)2+3,则抛物线y=5x2必须( )
| A、向左平移1个单位,再向下平移3个单位 |
| B、向右平移1个单位,再向上平移3个单位 |
| C、向右平移1个单位,再向下平移3个单位 |
| D、向左平移1个单位,再向上平移3个单位 |
 如图,在菱形ABCD中,对角线AC与BD相交于点O,点E是边AB的中点,CD=4,则OE的长是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,点E是边AB的中点,CD=4,则OE的长是( )| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
已知△ABC∽△DEF,AB=4,DE=8,若△ABC面积是6,则△DEF面积是( )
| A、12 | B、16 | C、24 | D、32 |




 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.