题目内容
6.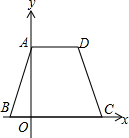 边BC在x轴上,点A在y轴的正方向上,A(0,6),D (4,6),且AB=2$\sqrt{10}$
边BC在x轴上,点A在y轴的正方向上,A(0,6),D (4,6),且AB=2$\sqrt{10}$(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,使得S△PBD=S梯形ABCD?若存在,请求出该点坐标;若不存在,请说明理由.
分析 (1)根据勾股定理即可求得;
(2)根据待定系数法即可求得;
(3)连接AC,并延长使EF=AC,过F点作PF∥BD,交抛物线于P,证得△AOC是等腰直角三角形,进一步证得△BEC和△AED是等腰直角三角形,通过三角形相似求得F的坐标,根据平行线的性质和待定系数法求得直线PF的解析式,解直线PF和抛物线解析式组成的方程组即可求得P的坐标.
解答 解:(1)∵A(0,6),
∴OA=6,
在Rt△OAB中,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{(2\sqrt{10})^{2}-{6}^{2}}$=2,
∴点B的坐标为(-2,0);
(2)设抛物线的解析式为y=ax2+bx+c,
把A(0,6),B(-2,0),D (4,6)代入,
得$\left\{\begin{array}{l}{c=6}\\{4a-2b+c=0}\\{16a+4b+c=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\\{c=6}\end{array}\right.$,
所以抛物线解析式为y=-$\frac{1}{2}$x2+2x+6;
(3)存在.
连接AC,并延长使EF=AC,过F点作PF∥BD,交抛物线于P,
∵OA=OC=6,
∴△AOC是等腰直角三角形,
∴∠ACB=45°,AC=6$\sqrt{2}$,
同理:∠DBC=45°,
∴AC⊥BD,
∴△BEC和△AED是等腰直角三角形,
∵AD=4,BC=8,
∴AE=2$\sqrt{2}$,
∵AC=EF,
∴CF=2$\sqrt{2}$,
作FG∥OA,
∴△AOC∽△FGC,
∴$\frac{FG}{OA}$=$\frac{CG}{OC}$=$\frac{CF}{AC}$,
∴FG=2,CG=2,
∴F(8,-2),
由B(-2,0),D(4,6),
设直线BD的解析式为y=kx+n,
∴$\left\{\begin{array}{l}{-2k+n=0}\\{4k+n=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{n=2}\end{array}\right.$,
设直线PF的解析式为y=x+m,
把F(8,-2)代入得,-2=8+m.解得m=-10,
∴直线PF的解析式为y=x-10,
解$\left\{\begin{array}{l}{y=x-10}\\{y=-\frac{1}{2}{x}^{2}+2x+6}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1+\sqrt{97}}{3}}\\{y=\frac{\sqrt{97}-29}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1-\sqrt{97}}{3}}\\{y=\frac{-29-\sqrt{97}}{3}}\end{array}\right.$,
∴P($\frac{1+\sqrt{97}}{3}$,$\frac{-29+\sqrt{97}}{3}$)或($\frac{1-\sqrt{97}}{3}$,$\frac{-29-\sqrt{97}}{3}$).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

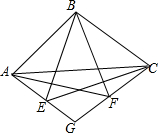 如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )| A. | ①②③ | B. | ①②③④ | C. | ①②④ | D. | ②③④ |
| A. | ±1 | B. | -1 | C. | 1 | D. | 0 |
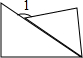 一副三角尺如图所示放置,使三角尺的30°角的顶点重合,且两直角三角尺的斜边重合,直角顶点在斜边的两侧,则∠1的度数是135°.
一副三角尺如图所示放置,使三角尺的30°角的顶点重合,且两直角三角尺的斜边重合,直角顶点在斜边的两侧,则∠1的度数是135°. 如图,长方形的长为(a+b),宽为(a-b),圆的半径为$\frac{1}{2}a$,求阴影部分的面积(π取3.14).
如图,长方形的长为(a+b),宽为(a-b),圆的半径为$\frac{1}{2}a$,求阴影部分的面积(π取3.14).