题目内容
12.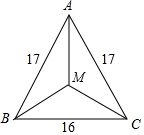 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )| A. | 10 | B. | $\sqrt{89}$ | C. | $\frac{136}{15}$ | D. | $\frac{289}{30}$ |
分析 根据在△ABC中,根据三线合一定理与勾股定理即可求得AN的长,然后根据重心的性质求得NM的长,即可求解.
解答  解:如图,延长AM,交BC于N点,
解:如图,延长AM,交BC于N点,
∵AB=AC,
∴△ABC为等腰三角形,
又∵M是△ABC的重心,
∴AN为中线,且AN⊥BC,
∴BN=CN=$\frac{16}{2}$=8,
AN=$\sqrt{1{7}^{2}-{8}^{2}}$=15,
MN=$\frac{1}{3}$AN=$\frac{1}{3}$×15=5,
∴CM=$\sqrt{M{N}^{2}+C{N}^{2}}$=$\sqrt{89}$
故选B.
点评 此题主要考查了重心的性质以及等腰三角形的三线合一性质和勾股定理等知识,根据重心性质得出AM=$\frac{2}{3}$AN是解题关键.

练习册系列答案
相关题目
14.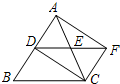 如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,延长DE至点F,使EF=DE,则四边形ADCF一定是( )
如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,延长DE至点F,使EF=DE,则四边形ADCF一定是( )
 如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,延长DE至点F,使EF=DE,则四边形ADCF一定是( )
如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,延长DE至点F,使EF=DE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 梯形 |
 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).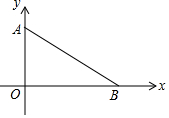 如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上
如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上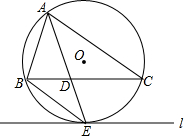 已知:如图,点A,B,C三点在⊙O上,AE平分∠BAC,交⊙O于点E,交BC于点D,过点E作直线l∥BC,连结BE.
已知:如图,点A,B,C三点在⊙O上,AE平分∠BAC,交⊙O于点E,交BC于点D,过点E作直线l∥BC,连结BE. 如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于B,且S△AOB=2,则k=4.
如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于B,且S△AOB=2,则k=4.