题目内容
2. 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).(1)写出△AOB的面积为3.5;
(2)点P在x轴上,当PA+PB的值最小时,在图中画出点P,并直接写出PA+PB的最小值为$\sqrt{29}$.
分析 (1)利用正方形的面积减去三个顶点上三角形的面积即可;
(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P点即为所求,利用勾股定理求出A′P的长即可.
解答 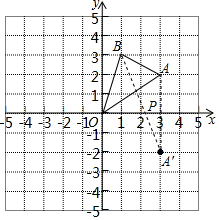 解:(1)S△ABC=3×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×1=9-3-$\frac{3}{2}$-1=3.5.
解:(1)S△ABC=3×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×1=9-3-$\frac{3}{2}$-1=3.5.
故答案为:3.5;
(2)如图,P点即为所求.
PA+PB=A′B=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$.
故答案为:$\sqrt{29}$.
点评 本题考查的是作图-应用与设计作图,根据题意作出点A的对称点A′是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.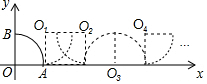 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )| A. | (16+4π,0) | B. | (14+4π,2) | C. | (14+3π,2) | D. | (12+3π,0) |
11.在下面的几何体中,俯视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.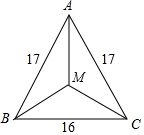 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )| A. | 10 | B. | $\sqrt{89}$ | C. | $\frac{136}{15}$ | D. | $\frac{289}{30}$ |
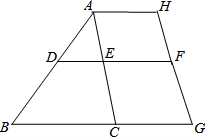 如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.
如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.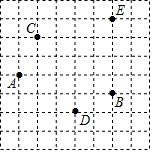 如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.
如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.