题目内容
14．
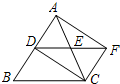如图，在△ABC中，AC=BC，点D，E分别是边AB，AC的中点，延长DE至点F，使EF=DE，则四边形ADCF一定是（ ）| A． | 矩形 | B． | 菱形 | C． | 正方形 | D． | 梯形 |
分析 先证明四边形ADCF是平行四边形，再证明AC=DF即可．
解答 解：∵E是AC中点，
∴AE=EC，
∵DE=EF，
∴四边形ADCF是平行四边形，
∵AD=DB，AE=EC，
∴DE=$\frac{1}{2}$BC，
∴DF=BC，
∵CA=CB，
∴AC=DF，
∴四边形ADCF是矩形；
故选：A．
点评 本题考查了矩形的判定、等腰三角形的性质、平行四边形的判定、三角形中位线定理；熟记对角线相等的平行四边形是矩形是解决问题的关键．
练习册系列答案
相关题目
11．在下面的几何体中，俯视图为三角形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．
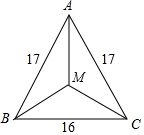如图，△ABC中，AB=AC=17，BC=16，M是△ABC的重心，CM的长度是（ ）
如图，△ABC中，AB=AC=17，BC=16，M是△ABC的重心，CM的长度是（ ）| A． | 10 | B． | $\sqrt{89}$ | C． | $\frac{136}{15}$ | D． | $\frac{289}{30}$ |
2．如果点A是线段BC外任意一点，则（ ）
| A． | AB+AC＜BC | B． | AB+AC=BC | C． | AB+AC＞BC | D． | AB+AC≥BC |
9．
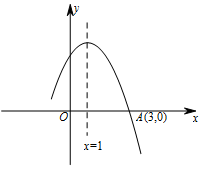如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，图象过A点（3，0），对称轴为x=1，给出六个结论：
①a+b+c=0；②b＞2a；③ax2+bx+c=0的两根分别为-1和3；④8a+c＜0；
⑤a-2b+4c＞0；⑥a+b＞m（am+b）
其中正确的结论是（ ）
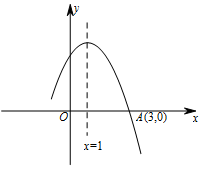如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，图象过A点（3，0），对称轴为x=1，给出六个结论：①a+b+c=0；②b＞2a；③ax2+bx+c=0的两根分别为-1和3；④8a+c＜0；
⑤a-2b+4c＞0；⑥a+b＞m（am+b）
其中正确的结论是（ ）
| A． | ①②④⑤⑥ | B． | ②③⑤⑥ | C． | ②③④⑤ | D． | ①③④⑥ |
19．
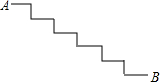如图，是台阶的示意图．已知每个台阶的宽度都是20cm，每个台阶的高度都是10cm，连接AB，则AB等于（ ）
如图，是台阶的示意图．已知每个台阶的宽度都是20cm，每个台阶的高度都是10cm，连接AB，则AB等于（ ）| A． | 120cm | B． | 130cm | C． | 140cm | D． | 150cm |
