题目内容
3.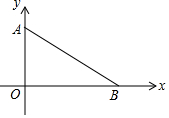 如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上
如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若函数y=$\frac{k}{x}$的图象经过点M,且sin∠OAB=$\frac{4}{5}$,求k的值.
分析 (1)作AB的垂直平分线交AB于点M,此时点M到点A,点B和原点O这三点的距离相等.
(2)利用勾股定理可求出点B的坐标,由(1)可知:M是AB的中点,从而可求出M的坐标.
解答  解:(1)点M为所求作;
解:(1)点M为所求作;
(2)∵sin∠OAB=$\frac{4}{5}$,
∴设OB=4x,AB=5x,
∴由勾股定理可知:32+(4x)2=(5x)2,
∴x=1,
∴OB=4,
由作图可知M为AB的中点,
∴M(2,$\frac{3}{2}$),
将M的坐标代入y=$\frac{k}{x}$中,
∴k=2×$\frac{3}{2}$=3,
点评 本题考查反比例函数的综合问题,解题的关键是求出B的坐标,利用M是AB的中点求出M的坐标,本题属于中等题型

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在下面的几何体中,俯视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.在下面的四个几何体中,它们各自的左视图与主视图不相同的是( )
| A. |  正方体 | B. |  三棱柱 | C. | 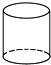 圆柱 | D. | 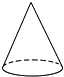 圆锥 |
12.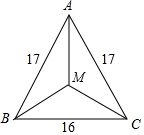 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,CM的长度是( )| A. | 10 | B. | $\sqrt{89}$ | C. | $\frac{136}{15}$ | D. | $\frac{289}{30}$ |
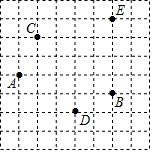 如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.
如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.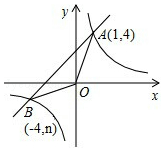 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).