题目内容
10. 如图,C为线段AB上一动点,分别过点A、B作DA⊥AB,EB⊥AB.已知AD=3,BE=2,AB=12,设AC=x
如图,C为线段AB上一动点,分别过点A、B作DA⊥AB,EB⊥AB.已知AD=3,BE=2,AB=12,设AC=x(1)用含x的代数式表示DC+CE的长.
(2)请问点C满足什么条件时,DC+CE的值最小?
(3)根据(2)的规律和结论,请构图求出代数式$\sqrt{{x^2}+25}+\sqrt{{{(8-x)}^2}+1}$的最小值.
分析 (1)由于△ADC和△CBE都是直角三角形,故DC,CE可由勾股定理求得;
(2)根据两点之间线段最短可知:当D、C、E三点共线时,DC+CE的值最小;
(3)由(1)(2)的结果可作AB=8,过点B作BE⊥AB,过点A作AD⊥AB,使AD=5,EB=1,连接DE交AB于点C,则DE的长即为代数式$\sqrt{{x}^{2}+25}+\sqrt{(8-x)^{2}+1}$的最小值,然后构造矩形AFEB,得到Rt△AFE,利用矩形的性质和勾股定理可求得DE的值.
解答 解:(1)∵DA⊥AB,EB⊥AB,
∴△ADC和△CBE都是直角三角形.
由勾股定理可知:DC+CE=$\sqrt{A{D}^{2}+A{C}^{2}}+\sqrt{B{E}^{2}+C{B}^{2}}$=$\sqrt{{3}^{2}+{x}^{2}}+\sqrt{(12-x)^{2}+{2}^{2}}$=$\sqrt{{x}^{2}+9}+\sqrt{(12-x)^{2}+4}$;
(2)根据两点之间线段最短可知:当D、C、E三点共线时,AC+CE的值最;
(3)如下图所示:作AB=8,过点B作BE⊥AB,过点A作AD⊥AB,使AD=5,EB=1,连接DE交AB于点C,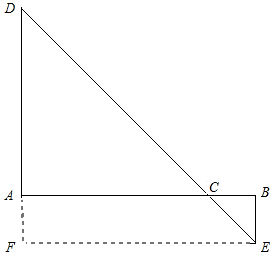
设AC=x,则DE的长即为代数式$\sqrt{{x}^{2}+25}+\sqrt{(8-x)^{2}+1}$的最小值.
过点E作EF∥AB交DA的延长线于点F,得矩形ABEF,
则AB=EF=8,AF=BE=1,DF=AD+AF=5+1=6,
在Rt△DFE中,由勾股定理得:DE=$\sqrt{D{F}^{2}+E{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}=10$,
即代数式$\sqrt{{x}^{2}+25}+\sqrt{(8-x)^{2}+1}$的最小值为10.
点评 本题综合考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,解题时,注意作图所依据的公理以及相关图形的性质.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | 矩形 | B. | 菱形 | C. | 平行四边形 | D. | 正五边形 |
 如图,AB是半圆O的直径,点P从点O出发,沿OA→$\widehat{AB}$→BO的路径运动一周,设点P到点O的距离为S,运动时间为t,则下列图形能大致地刻画S与t之间的关系的是( )
如图,AB是半圆O的直径,点P从点O出发,沿OA→$\widehat{AB}$→BO的路径运动一周,设点P到点O的距离为S,运动时间为t,则下列图形能大致地刻画S与t之间的关系的是( )| A. | 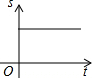 | B. | 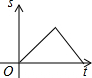 | C. |  | D. |  |

 在Rt△ABC中,∠C=90°,AB=4,∠ABC=30°,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOB=∠COB=120°,按下列要求画图:以点B为旋转中心,将△AOB绕点B逆时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),回答下列问题:
在Rt△ABC中,∠C=90°,AB=4,∠ABC=30°,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOB=∠COB=120°,按下列要求画图:以点B为旋转中心,将△AOB绕点B逆时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),回答下列问题: 如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG,⑤BH=HG.其中正确的结论是( )
如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG,⑤BH=HG.其中正确的结论是( ) 已知,如图,在直角坐标系中,点M(2,2),一直角三角板直角顶点与点M重合,两直角边分别与x轴正半轴、y轴正半轴交于点A、B,则OA+OB的值是否会发生变化?若不变,求出其值;若变化,求其变化的范围.
已知,如图,在直角坐标系中,点M(2,2),一直角三角板直角顶点与点M重合,两直角边分别与x轴正半轴、y轴正半轴交于点A、B,则OA+OB的值是否会发生变化?若不变,求出其值;若变化,求其变化的范围.